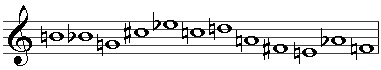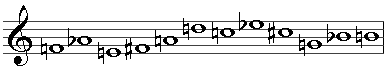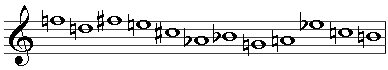Twelve-tone technique
|
|
Twelve-tone technique (also dodecaphony) is a system of musical composition devised by Arnold Schoenberg. Music using the technique is called twelve-tone music. Josef Matthias Hauer also developed a similar system using unordered hexachords, or tropes, at the exact same time and country but with no connection to Schoenberg.
Schoenberg himself described the system as a "method of composing with 12 notes which are related only to one another".
| Contents |
The technique
The basis of twelve-tone technique is the tone row or set, an ordered arrangement of the twelve notes of the chromatic scale (the twelve equal tempered pitch classes), or, rather, an ordered arrangement of intervals which produce those notes. When the technique is applied most rigorously, an entire piece must be built up from statements of any transposition of this tone row in strict order or transformations of this row. Both melody and harmony may be created in this way. The set may be used in succession or simultaneously, the latter of which may be ordered up or down, or not. Given twelve pitch classes, there are 12! (12 factorial) possible tone rows, though invariance often reduces the number of distinct rows.
The initial tone row, or set form, used is called the prime series (P), untransposed it is P0. P can be used starting on any one of the twelve notes of the chromatic scale (Pχ) - so long as the intervals are the same, the rows are equivalent. Pχ = P0 + χ.
Additionally, P can be transformed in three basic ways: it can be turned backwards to get the retrograde (R) or turned upsidedown to give the inversion (I) or the reverse contour direction. I(χ) = 12 - Pχ. These three transformative techniques can be combined to give the retrograde inversion (RI). As with the prime series, R, I and RI can be transposed to any note of the chromatic scale.
| RI is: | RI of P, | R of I, | and I of R. |
| R is: | R of P, | RI of I, | and I of RI. |
| I is: | I of P, | RI of R, | and R of RI. |
| P is: | R of R, | I of I, | and RI of RI. |
thus:
| P: | RI: | R: | I: |
| RI: | P | I | R |
| R: | I | P | RI |
| I: | R | RI | P |
More recently composers such as Charles Wuorinen have also used multiplication of the row. However, there are only a few numbers which one may multiply a row by and still end up with twelve tones. Multiplication is indicated by MX, X being the multiplier. As with the other compound operations multiplication is carried out and then transposition. P0 = M10, I0 = M110, M70=I(M50). Thus, for the untransposed form of all:
| M1: | M5: | M7: | M11: |
| M5: | M1 | M11 | M7 |
| M7: | M11 | M1 | M5 |
| M11: | M7 | M5 | M1 |
Even numbers remain unchanged under M7 and all odd numbers become transposed by a tritone. The chromatic scale may be mapped onto the circle of fourths with M5, and the circle of fifths with M7.
Suppose the prime series is as follows:
Then the retrograde is the prime series in reverse order:
The inversion is the prime series with the intervals inverted (so that a rising minor third becomes a falling minor third):
Missing image
Inversion_tone_row.png
B, C, Eb, A, G, Bb, Ab, C#, E, F#, D, F
And the retrograde inversion is the inverted series in retrograde:
P, R, I and RI can each be started on any of the twelve notes of the chromatic scale, meaning that 47 permutations of the initial tone row can be used, giving a maximum of 48 possible tone rows. However, not all prime series will yield so many variations because tranposed transformations may be identical to each other. This is known as invariance. A simple case is the ascending chromatic scale, the retrograde inversion of which is identical to the prime form, and the retrograde of which is identical to the inversion (thus, only 24 forms of this tone row are available).
When rigorously applied, the technique demands that one statement of the tone row must be heard in full (otherwise known as aggregate completion) before another can begin. Adjacent notes in the row can be sounded at the same time, and the notes can appear in any octave, but the order of the notes in the tone row must be maintained. Durations, dynamics and other aspects of music other than the pitch can be freely chosen by the composer, and there are also no rules about which tone rows should be used at which time (beyond them all being derived from the prime series, as already explained).
Schoenberg's idea in developing the technique was for it to act as a replacement for tonal harmony as a basic grounding force for music. As such, twelve-tone music is usually atonal, and treats each of the 12 semitones of the chromatic scale with equal importance, as opposed to earlier classical music which had treated some notes as more important than others (particularly the tonic and the dominant note).
History of the technique's use
Founded by Austrian composer Arnold Schoenberg around the late 1910s, the method was used during the next 20 years almost exclusively by the Second Viennese School (Alban Berg, Anton Webern, Hanns Eisler and Arnold Schoenberg himself). Rudolph Reti, an early proponent says: "To replace one structural force (tonality) by another (increased thematic oneness) is indeed the fundamental idea behind the twelve-tone technique," arguing it arose out of Schoenberg's frustrations with free atonality (Reti, 1958). The technique became widely used by the fifties, taken up by composers such as Luciano Berio, Pierre Boulez, Luigi Dallapiccola and, after Schoenberg's death, Igor Stravinsky. Some of these composers extended the technique to control aspects other than the pitches of notes (such as duration, method of attack and so on), thus producing serial music. Some even subjected all elements of music to the serial process.
In practice, the "rules" of twelve-tone technique have been bent and broken many times, not least by Schoenberg himself. For instance, in some pieces two or more tone rows may be heard progressing at once, or there may be parts of a composition which are written freely, without recourse to the twelve-tone technique at all. Offshoots or variations may produce music in which:
- the full chromatic is used and constantly circulates, but permutational devices are ignored
- permutational devices are used but not on the full chromatic
Charles Wuorinen claimed in a 1962 interview that while, "most of the Europeans say that they have 'gone beyond' and 'exhausted' the twelve-tone system," in America, "the twelve-tone system has been carefully studied and generalized into an edifice more impressive than any hitherto known." (Chase 1992, p.587)
Derivation
Derivation is transforming segments of the full chromatic, less than 12 pitch classes, to yield a complete set, most commonly using trichords, tetrachords, and hexachords. A derived set can be generated by choosing appropriate transformations of any trichord except 0,3,6, the diminished triad. A derived set can also be generated from any tetrachord that excludes the interval class 4, a major third, between any two elements. The opposite is partitioning, the use of methods to create segments from sets, most often through registral difference.
Combinatoriality
Combinatoriality is a side-effect of derived rows where combining different segments or sets such that the pitch class content of the result fulfills certain criteria, usually the combination of hexachords which complete the full chromatic.
Invariance
Invariant formations are also the side effect of derived rows where a segment of a set remains similar or the same under transformation. These may be used as "pivots" between set forms, sometimes used by Anton Webern, see George Perle.
Other
Also, some composers have used cyclic permutation, or rotation, where the row is taken in order but using a different starting note.
Although usually atonal, twelve tone music need not be - several pieces by Berg, for instance, have tonal elements.
One of the best known twelve-note compositions is Variations for Orchestra by Arnold Schoenberg. "Quiet", in Leonard Bernstein's Candide, satirizes the method by using it for a song about boredom.
Further reading
- Serial Composition and Atonality: An Introduction to the Music of Schoenberg, Berg, and Webern by George Perle, ISBN 0520074300
- Simple Composition by Charles Wuorinen, ISBN 0938856065.
Sources
- Chase, Gilbert (1992). America's Music: From the Pilgrims to the Present. University of Illinois Press, ISBN 0252062752.
- Reti, Rudolph (1958). Tonality, Atonality, Pantonality: A study of some trends in twentieth century music. Westport, Connecticut: Greenwood Press. ISBN 0313204780.
External links
- New Transformations: Beyond P, I, R, and RI by Larry Solomon (http://wc.pima.edu/%7Elsolomon/diss8.htm)
- Set Theory Glossary (http://music.theory.home.att.net/setgloss.htm)
- Twelve tone techniques (http://www.cwu.edu/~compose/PostTonal_5.html)de:Zwölftonmusik
es:Música dodecafónica fr:Dodécaphonisme nl:Dodecafonie ja:十二音技法 pl:Dodekafonia pt:Dodecafonismo