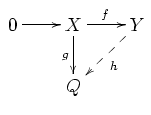Injective module
|
|
In mathematics, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers. Specifically, if Q is a submodule of some other module, then it is already a direct summand of that module; also, given a submodule of a module Y, then any module homomorphism from this submodule to Q can be extended to a homomorphism from all of Y to Q. This concept is dual to that of projective modules. Injective modules were introduced by Reinhold Baer in 1940.
| Contents [hide] |
Definition
More formally, a left module Q over the ring R is injective if it satisfies one (and therefore all) of the following equivalent conditions:
- If Q is a submodule of some other left R-module M, then there exists another submodule K of M such that M is the internal direct sum of Q and K, i.e. Q + K = M and Q ∩ K = {0}.
- If X is a submodule of the left R-module Y and g : X → Q is a module homomorphism, then there exists a module homomorphism h : Y → Q such that h(x) = g(x) for all x in X.
- If X and Y are left-R modules and f : X → Y is an injective module homomorphism and g : X → Q is an arbitrary module homomorphism, then there exists a module homomorphism h : Y → Q such that hf = g, i.e. such that the following diagram commutes:
- Any short exact sequence 0 →Q → M → K → 0 of left R-modules splits.
- The contravariant functor Hom(-,Q) from the category of left R-modules to the category of abelian groups is exact.
Injective right R-modules are defined in complete analogy.
Examples
Trivially, the zero module {0} is injective.
Every vector space Q is injective. Reason: if Q is a subspace of V, we can find a basis of Q and extend it to a basis of V. The new extending basis vectors span a subspace K of V and V is the internal direct sum of Q and K. Note that the direct complement K of Q is not uniquely determined by Q, and likewise the extending map g in the above definition is typically not unique.
If G is a finite group and k a field with characteristic 0, then one shows in the theory of group representations that any subrepresentation of a given one is already a direct summand of the given one. Translated into module language, this means that all modules over the group algebra kG are injective. If the characteristic of k is not zero, the following example may help.
If A is a unital associative algebra over the field k with finite dimension over k, then Homk(−, k) is a duality between finitely generated left A-modules and finitely generated right A-modules. Therefore, the finitely generated injective left A-modules are precisely the modules of the form Homk(P, k) where P is a finitely generated projective right A-module.
Over other rings, injective modules are abundant, but it is not easy to come up with examples without some theory (mentioned below). The rationals Q (with addition) form an injective abelian group (i.e. an injective Z-module). The factor group Z/nZ for n > 1 is injective as a Z/nZ-module, but not injective as an abelian group.
Facts
Any product of (even infinitely many) injective modules is injective. Every direct sum of finitely many injective modules is injective. In general, submodules, factor modules or infinite direct sums of injective modules need not be injective.
In Baer's original paper, he proved a useful result, usually known as Baer's Criterion, for checking whether a module is injective: a left R-module Q is injective if and only if any homomorphism g : I → Q defined on a left ideal I of R can be extended to all of R.
Using this criterion, one can show that Q is an injective abelian group (i.e. an injective module over Z). More generally, an abelian group is injective if and only if it is divisible. More generally still: a module over a principal ideal domain is injective if and only if it is divisible. One may view the example about vector spaces as a special case of this theorem, as every vector space is divisible.
Maybe the most important injective module is the abelian group Q/Z. It is an injective cogenerator in the category of abelian groups, which means that it is injective and any other module is contained in a suitably large product of copies of Q/Z. So in particular, every abelian group is subgroup of an injective one. It is quite significant that this is also true over any ring: every module is a submodule of an injective one, or "the category of left R-modules has enough injectives." To prove this, one uses the peculiar properties of the abelian group Q/Z to construct an injective cogenerator in the category of left R-modules.
One can then go on to define the injective hull of a module (essentially the smallest injective module containing the given one). Every module M also has an injective resolution: an exact sequences of the form
- 0 → M → I0 → I1 → I2 → ...
where the Ij are injective. These injective resolutions are used to define the injective dimension of a module (the length of the shortest injective resolution ending in zeros, if such a finite resolution exists) as well as derived functors.
Every indecomposable injective module has a local endomorphism ring.
Generalization
One also talks about injective objects in categories more general than module categories, for instance in functor categories or in categories of sheaves of OX modules over some ringed space (X,OX). The following general definition is used: an object Q of the category C is injective if for any monomorphism f : X → Y in C and any morphism g : X → Q there exists a morphism h : Y → Q with hf = g.
References
- F.W. Anderson and K.R. Fuller: Rings and Categories of Modules, Graduate Texts in Mathematics, Vol. 13, 2nd Ed., Springer-Verlag, New York, 1992.es:Módulo inyectivo