Floyd's cycle-finding algorithm
|
|
Floyd's cycle-finding algorithm is an algorithm invented by Robert W. Floyd in 1967 which can detect cycles in arbitrary sequences, whether in data structures or generated on the fly, notably including those in graphs and pseudo-random sequences in O(1) space.
Sometimes called "tortoise and the hare" -- an apt description. Inkoka matallo "Taabelu mariyu kundelu"-- sariyana vivarana.
The following discussion is couched in terms of pseudo-random sequences in particular, of great importance in analyzing pseudo-random number generators and in applications to factoring algorithms such as Pollard Rho.
Let
- <math>f\colon S\mapsto S<math>
be a pseudo-random function, with S a finite set of cardinality n. Define a sequence ai as:
- <math>a_{i+1}=f(a_i)<math>
Clearly such a sequence must cycle after at most n iterations of the pseudo-random function, because there are only n possible values for an element. The naïve way to find the length of the cycle is to store each element of the sequence and, at each iteration, look among all the stored elements for duplicates. This means that the storage requirement is O(μ + λ), where μ is the length of the cycle and λ is the length of the tail (i.e. the part of the sequence that does not cycle).
Note that if we find two elements of the sequence such that
- <math>a_i=a_{j}<math>
then |i − j| must be a multiple of the cycle length, because of the definition of a cycling sequence:
- <math>a_{\lambda+m}=a_{\lambda+m+k\mu}.<math>
The difference of the two indices that hold equal elements is kμ, a multiple of the cycle length. Floyd's cycle-finding algorithm finds such an equality by running two instances of the sequence in parallel, one twice as "fast" as the other; i.e. one instance undergoes two iterations while the other undergoes one. Then, when
- <math>a_m=a_{2m}<math>
then any divisor of 2m − m = m might be the length of the cycle. If m is composite, one can let the algorithm continue running until it finds more values of m for which the above equality is true, and take the greatest common divisor of the m's. This way, the list of possible μ's can be trimmed.
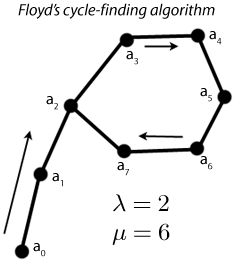
The best way to visualize this algorithm is to make a diagram of the sequence. It looks like the Greek letter ρ. The sequence starts at the bottom of the "tail", and moves upward and clockwise around the loop. Following the algorithm, the two instances of the sequence will meet at a6 after six iterations. If the algorithm keeps running, the sequences will meet again, after six more iterations, at the same element. Since the cycle length is in fact six, the same result will keep occurring.The best performance this algorithm can give is λ comparisons (with λ > 1), since the "slow" sequence has to get at least to the beginning of the cycling part. The worst-case performance is λ + μ/2 comparisons; the slow sequence cannot get more than halfway around the loop without meeting the fast sequence. The algorithm uses O(1) storage.
Perhaps the most widely known variant of Floyd's cycle-finding algorithm is Pollard's rho algorithm, an integer factorization algorithm that uses pseudo-random sequences to factor integers. There is also an algorithm for calculating discrete logarithms based on Floyd's cycle-finding algorithm.
Apparently first published in: "Non-deterministic Algorithms", R. W. Floyd, J. Assoc.Computing, pp. 636-644, March 1967.
Note that "Floyd's Algorithm" is not quite the same as "Floyd's Cycle-Finding Algorithm", although they are loosely related, and due to the same author.