Continuous function (topology)

In topology and related areas of mathematics a continuous function is a morphism between topological spaces, that is a mapping which preserves the topological structure.

Given a set X a partial ordering can be defined on the possible topologies on X. Surjective continuous functions between topological spaces are only possible if the topology of the codomain space is weaker than the topology of the domain space. Thus we can consider the continuity of a given function a topological property, depending only on the topologies of its domain and codomain spaces. A continuous function can be visualized as weakening the topology of the domain space.

In real analysis continuity of functions is commonly defined using the ε-δ definition which builds on the property of the real line being a metric space. As topological spaces generally do not have this property a more general definition is needed which reduces to the ε-δ definition in case of the real line.

Contents

1 Definitions 1.1 Open and closed set definition 1.2 Neighborhood definition 1.3 Closure and interior operator definition 1.4 Closeness relation definition 2 Useful properties of continuous maps 3 Other notes

Definitions

Several equivalent definitions for a topological structure exist and thus there are several equivalent ways to define a continuous function.

Open and closed set definition

The most common one defines continuous functions as those functions where the preimages of open sets are open. Similar to the open set formulation is the closed set formulation, which says that preimages of closed sets are closed.

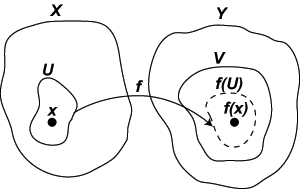
Neighborhood definition

Definition based on preimages are often difficult to use directly. Instead, suppose we have a function f from X to Y, where X,Y are topological spaces. We say f is continuous at x for some <math>x \in X<math> if for any neighborhood V of f(x), there is a neighborhood U of x such that <math>f(U) \subseteq V<math>. Although this definition appears complex, the intuition is that no matter how "small" V becomes, we can find a small U containing x that will map inside it. If f is continuous at every <math>x \in X<math>, then we simply say f is continuous.

In a metric space, it is equivalent to consider the neighbourhood system of open balls centered at x and f(x) instead of all neighborhoods. This leads to the standard ε-δ definition of a continuous function from real analysis, which says roughly that a function is continuous if all points close to x map to points close to f(x). This only really makes sense in a metric space, however, which has a notion of distance.

Closure and interior operator definition

Given two topological spaces (X,cl) and (X ' ,cl ') where cl and cl ' are two closure operators then a function

<math>f:(X,\mathrm{cl}) \to (X' ,\mathrm{cl}')<math>

is continuous if for all subsets A of X

<math>f(\mathrm{cl}(A)) \subseteq \mathrm{cl}'(f(A)).<math>

Similarily given two topological spaces (X,int) and (X ' ,int ') where int and int ' are two interior operators then a function

<math>f:(X,\mathrm{int}) \to (X' ,\mathrm{int}')<math>

is continuous if for all subsets A of X

<math>f(\mathrm{int}(A)) \subseteq \mathrm{int}'(f(A)).<math>

Closeness relation definition

Given two topological spaces (X,δ) and (X ' ,δ ') where δ and δ ' are two closeness relations then a function

<math>f:(X,\delta) \to (X' ,\delta')<math>

is continuous if for all points x and y of X

<math>x \delta y \Leftrightarrow f(x)\delta'f(y).<math>

Useful properties of continuous maps

Some facts about continuous maps between topological spaces:

• If f : X → Y and g : Y → Z are continuous, then so is the composition g o f : X → Z.
• If f : X → Y is continuous and
  • X is compact, then f(X) is compact.
  • X is connected, then f(X) is connected.
  • X is path-connected, then f(X) is path-connected.

• If f : X → Y is continuous and a sequence (x_n) in X converges to a limit x, then the sequence (f(x_n)) obtained by applying f to each element converges to f(x). We say continuous functions take limits to limits. This also holds if sequences are replaced by general nets.
  • If X is a metric space, then the converse also holds: any function taking limits to limits is continuous. When using nets instead of sequences, this converse holds for a general topological space X.

Other notes

If a set is given the discrete topology, all functions with that space as a domain are continuous. If the domain set is given the indiscrete topology and the range set is at least T₀, then the only continuous functions are the constant functions. Conversely, any function whose range is indiscrete is continuous.

Symmetric to the concept of a continuous map is an open map, for which images of open sets are open. In fact, if an open map f has an inverse, that inverse is continuous, and if a continuous map g has an inverse, that inverse is open.

If a function is a bijection, then it has an inverse function. The inverse of a continuous bijection need not be continuous, but if it is, this special function is called a homeomorphism.de:Stetigkeit (Topologie)