Antiprism
|
|
| Pentagonal antiprism | |
|---|---|
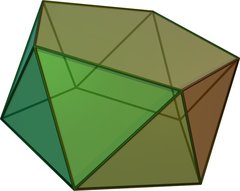 Click on picture for large version. | |
| Heptadecagonal antiprism | |
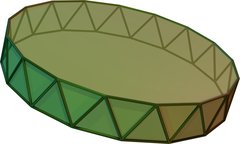 Click on picture for large version. | |
| Type | Antiprism |
| Faces | 2 n-gons, 2n triangles |
| Edges | 4n |
| Vertices | 2n |
| Vertex configuration | n,3,3,3 |
| Symmetry group | Dnd |
| Dual polyhedron | trapezohedron |
| Properties | convex, semi-regular (vertex-uniform) |
An antiprism is a polyhedron composed of two parallel copies of some particular polygon, connected by an alternating band of triangles.
Antiprisms are similar to prisms except the bases are twisted relative to each other. Regular right antiprisms form an infinite series of vertex-uniform polyhedra, as do the regular right prisms. The octahedron is a particular type of right triangular antiprism which is also edge- and face-uniform, and so counts among the Platonic solids. The dual polyhedra of the antiprisms are the trapezohedra. Their existence was first discussed and their name was coined by Johannes Kepler.
Canonical coordinates for an antiprism with n-gons are (sin(2πk/n), cos(2πk/n), ±a) with k ranging from 0 to n-1, where
- <math>a=\sqrt{\frac{\cos\frac{\pi}{n}-\cos\frac{2\pi}{n}}{2}}<math>.
External links
- Paper models of prisms and antiprisms (http://www.software3d.com/Prisms.html)
- The Uniform Polyhedra (http://www.mathconsult.ch/showroom/unipoly/)
- Virtual Reality Polyhedra (http://www.georgehart.com/virtual-polyhedra/vp.html) The Encyclopedia of Polyhedra
