Aharonov-Bohm effect
|
|
The Aharonov-Bohm effect is a quantum mechanical phenomenon by which a charged particle is affected by electromagnetic fields in regions from which the particle is excluded, proposed by Aharonov and Bohm in 1959. Such effects are predicted to arise from both magnetic fields and electric fields, but the magnetic version has been easier to observe. In general, the profound consequence of Aharonov-Bohm effects is that knowledge of the classical electromagnetic field acting locally on a particle is not sufficient to predict its quantum-mechanical behavior.
After the 1959 paper was published, Bohm was informed that the effect had been predicted by Rory E. Siday and Werner Ehrenberg a decade earlier; Bohm and Aharonov duly cited this in their second paper (Peat, 1997, p. 192).
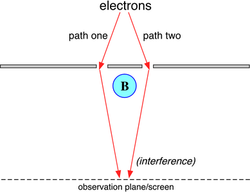
The most commonly described case, sometimes called the Aharonov-Bohm solenoid effect, is where a charged particle passing around a long solenoid experiences a quantum phase shift as a result of the enclosed magnetic field, despite the magnetic field being zero in the region through which the particle passes. This phase shift has been observed experimentally by its effect on interference fringes. (There are also magnetic Aharonov-Bohm effects on bound energies and scattering cross sections, but this case has not been experimentally tested.) An electric Aharonov-Bohm phenomenon was also predicted, in which a charged particle is affected by regions with different electrical potentials but zero electric field, and this has also seen experimental confirmation. A separate "molecular" Aharonov-Bohm effect was proposed for nuclear motion in multiply-connected regions, but this has been argued to be essentially different, depending only on local quantities along the nuclear path.
| Contents |
Magnetic Aharonov-Bohm effect
The magnetic Aharonov-Bohm effect can be seen as a result of the requirement that quantum physics be invariant with respect to the gauge choice for the vector potential A. This implies that a particle with charge q travelling along some path P in a region with zero magnetic field (<math>\mathbf{B} = 0 = \nabla \times \mathbf{A}<math>) must acquire a phase φ given in SI units by
- <math>\phi = \frac{q}{\hbar} \int_P \mathbf{A} \cdot d\mathbf{x},<math>
with a phase difference Δφ between any two paths with the same endpoints therefore determined by the magnetic flux Φ through the area between the paths (via Stokes theorem and <math>\nabla \times \mathbf{A} = \mathbf{B}<math>), and given by:
- <math>\Delta\phi = \frac{q\Phi}{\hbar}.<math>
This phase difference can be observed by placing a solenoid between the slits of a double-slit experiment (or equivalent). A solenoid encloses a magnetic field B, but does not produce any magnetic field outside of its cylinder, and thus the charged particle (e.g. an electron) passing outside experiences no classical effect. However, there is a (curl-free) vector potential outside the solenoid with an enclosed flux, and so the relative phase of particles passing through one slit or the other is altered by whether the solenoid current is turned on. This corresponds to an observable shift of the interference fringes on the observation plane.
The same phase effect is responsible for the quantized-flux requirement in superconducting loops. This quantization is due to the fact that the superconducting wave function must be single valued: its phase difference Δφ around a closed loop must be an integer multiple of 2π (with the charge q=2e for the electron Cooper pairs), and thus the flux Φ must be a multiple of h/2e. The superconducting flux quantum was actually predicted prior to Aharonov and Bohm, by London in 1948 using a phenomenological model.
The magnetic Aharonov-Bohm effect is also closely related to Dirac's argument that the existence of a magnetic monopole necessarily implies that both electric and magnetic charges are quantized. A magnetic monopole implies a mathematical singularity in the vector potential, which can be expressed as an infinitely long Dirac string of infinitesimal diameter that contains the equivalent of all of the 4πg flux from a monopole "charge" g. Thus, assuming the absence of an infinite-range scattering effect by this arbitrary choice of singularity, the requirement of single-valued wave functions (as above) necessitates charge-quantization: <math>2qg/c\hbar<math> must be an integer (in cgs units) for any electric charge q and magnetic charge g.
Electric Aharonov-Bohm effect
Just as the phase of the wave function depends upon the magnetic vector potential, it also depends upon the scalar electric potential. By constructing a situation in which the electrostatic potential varies for two paths of a particle, through regions of zero electric field, an observable Aharonov-Bohm interference phenomenon from the phase shift has been predicted; again, the absence of an electric field means that, classically, there would be no effect.
From the Schrödinger equation, the phase of an eigenfunction with energy E goes as <math>\exp(-iEt/\hbar)<math>. The energy, however, will depend upon the electrostatic potential V for a particle with charge q. In particular, for a region with constant potential V (zero field), the electric potential energy qV is simply added to E, resulting in a phase shift:
- <math>\Delta\phi = -\frac{qVt}{\hbar} ,<math>
where t is the time spent in the potential.
The initial theoretical proposal for this effect suggested an experiment where charges pass through conducting cylinders along two paths, which shield the particles from external electric fields in the regions where they travel, but still allow a varying potential to be applied by charging the cylinders. This proved difficult to realize, however. Instead, a different experiment was proposed involving a ring geometry interrupted by tunnel barriers, with a bias voltage V relating the potentials of the two halves of the ring. This situation results in an Aharonov-Bohm phase shift as above, and was observed experimentally in 1998.
Mathematical interpretation
In the terms of modern differential geometry, the Aharonov-Bohm effect can be understood to be the holonomy of the complex-valued line bundle representing the electromagentic field. The connection on the line bundle is given by the electromagnetic potential A, and thus the electromagnetic field strength is the curvature of the line bundle F=dA. The integral of A around a closed loop is the holonomy, which, by Stokes law, is the magentic field threading the loop. Thus the wave function of the electron can be seen to be directly coupled to the complex line bundle representing the electromagnetic field.
See also a related effect, the Berry phase.
References
- Y. Aharonov and D. Bohm, "Significance of electromagnetic potentials in quantum theory," Phys. Rev. 115, 485–491 (1959).
- S. Olariu and I. Iovitzu Popèscu, "The quantum effects of electromagnetic fluxes," Rev. Mod. Phys. 57, 339–436 (1985).
- M. Peshkin and A. Tonomura, The Aharonov-Bohm Effect (Springer-Verlag: Berlin, 1989).
- F. London, "On the problem of the molecular theory of superconductivity," Phys. Rev. 74, 562–573 (1948).
- F. David Peat (http://www.fdavidpeat.com/), Infinite Potential: The Life and Times of David Bohm (Addison-Wesley: Reading, MA, 1997). ISBN 0-201-40635-7.
- E. Sjöqvist, "Locality and topology in the molecular Aharonov-Bohm effect," Phys. Rev. Lett. 89 (21), 210401/1–3 (2002).
- A. van Oudenaarden, M. H. Devoret, Yu. V. Nazarov, and J. E. Mooij, "Magneto-electric Aharonov-Bohm effect in metal rings," Nature 391, 768–770 (1998).de:Aharonov-Bohm-Effekt