Convex function
|
|
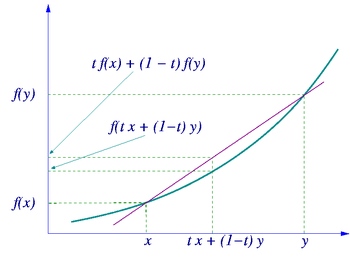
In mathematics, convex function is a real-valued function f defined on an interval (or on any convex subset C of some vector space), if for any two points x and y in its domain C and any t in [0,1], we have
- <math>f(tx+(1-t)y)\leq t f(x)+(1-t)f(y).<math>
I.e., a function is convex if and only if its epigraph (the set of points lying on or above the graph) is a convex set. A function is also said to be strictly convex if
- <math>f(tx+(1-t)y) < t f(x)+(1-t)f(y).\,\!<math>
for any t in (0,1).
| Contents |
Logarithmically convex function
A function <math>f<math> such that <math>f(x) > 0<math> for all <math>x<math> is said to be logarithmically convex function if <math>\log f(x)<math> is a convex function of <math>x<math>.
It is easy to see that a logarithmically convex function is a convex function, but the converse is not true. For example <math>f(x) = x^2<math> is a convex function, but <math>\log f(x) = \log x^2 = 2 \log x<math> is not a convex function and thus <math>f(x) = x^2<math> is not logarithmically convex. On the other hand <math>e^{x^2}<math> is logarithmically convex since <math>\log e^{x^2} = x^2<math> is convex. A less trivial example of a logarithmically convex function is the gamma function, if restricted to the positive reals. (See also Bohr-Mollerup theorem.)
The definition is easily extended to functions <math>f\colon \R \to \R<math> where still we have <math>f > 0<math>, in the obvious way. Such a function is logarithmically convex if it is logarithmically convex on all intervals <math>[a,b]<math>.
Properties of convex functions
A convex function f defined on some convex open interval C is continuous on the whole C and differentiable at all but at most countably many points. If C is closed, then f may fail to be continuous at the border.
A continuous function on C is convex if and only if
- <math>f\left( \frac{x+y}2 \right) \le \frac{f(x)+f(y)}2 .<math>
for any x and y in C.
A differentiable function of one variable is convex on an interval if and only if its derivative is monotonically non-decreasing on that interval.
A continuously differentiable function of one variable is convex on an interval if and only if the function lies above all of its tangents: f(y) ≥ f(x) + f'(x) (y − x) for all x and y in the interval.
A twice differentiable function of one variable is convex on an interval if and only if its second derivative is non-negative there; this gives a practical test for convexity. If its second derivative is positive then it is strictly convex, but the opposite is not true, as shown by f(x) = x4.
More generally, a continuous, twice differentiable function of multiple variables is convex on a convex set if and only if its Hessian matrix is positive semidefinite on the interior of the convex set.
If two functions f and g are convex, then so is any weighted combination a f + b g with non-negative coefficients a and b.
Any local minimum of a convex function is also a global minimum. A strictly convex function will have at most one global minimum.
For a convex function f, the level sets {x | f(x) < a} and {x | f(x) ≤ a} with a ∈ R are convex sets.
Convex functions respect Jensen's inequality.
Examples of convex functions
- The second derivative of x2 is 2; it follows that x2 is a convex function of x.
- The absolute value function |x| is convex, even though it does not have a derivative at x = 0.
- The function f(x) = x is convex but not strictly convex.
- The function x3 has second derivative 6x; thus it is convex for x ≥ 0 and concave for x ≤ 0.