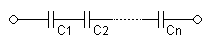Series and parallel circuits
|
|
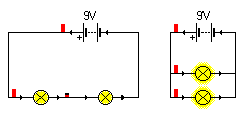
In electrical circuits series and parallel are two basic ways of wiring components. The naming comes after the method of attaching components, i.e. one after the other, or next to each other. As a demonstration, consider a very simple circuit consisting of two lightbulbs and one 9V battery. If a wire joins the battery to one bulb, to the next bulb, then back to the battery, in one continuous loop, the bulbs are said to be in series. If, on the other hand, each bulb is wired separately to the battery in two loops, the bulbs are said to be in parallel.
The measurable quantities used here are R, resistance, measured in ohms (Ω), I, current, measured in amperes (A) (coulombs per second), and V, voltage, measured in volts (V) (joules per coulomb).
| Contents |
Series circuits
Series circuits are sometimes called cascade-coupled or daisy chain-coupled.
The same current has to pass through all the components in the series. An ammeter placed anywhere in the circuit would measure the same amount.
Resistors
To find the total resistance of all the components, add together the individual resistances of each component;
- Missing image
Resistorsseries.png
A diagram of several resistors, connected end to end, with the same amount of current going through each
- <math>
R_{total} = R_1 + R_2 + \cdots + R_n <math>
- for components in series, having resistances R1, R2, etc.
To find the current, I, use Ohm's law.
- <math>
I = V / R_{total} <math>
To find the voltage across any particular component with resistance Ri, use Ohm's law again.
- <math>
V_i = I \cdot R_i <math>
- Where I is the current, as calculated above.
Note that the components divide the voltage according to their resistances, so, in the case of two resistors:
- <math>
V_1 / V_2 = R_1 / R_2 <math>
Inductors
Inductors follow the same law, in that the total inductance of non-coupled inductors in series is equal to the sum of their individual inductances:
- Missing image
Inductorsseries.png
A diagram of several inductors, connected end to end, with the same amount of current going through each
- <math>L_{total} = L_1 + L_2 + \cdots + L_n<math>
However, stating it like that would be too simple. Inductors will influence each other. This influence is defined by the mutual inductance M. For example, if you have two inductors in series, there are two possible equivalent inductances:
- <math>L_{total} = (L_1 + M) + (L_2 + M)<math> or
- <math>L_{total} = (L_1 - M) + (L_2 - M)<math>
Which formula is the correct one, depends how the magnetic fields of both inductors influence each other.
When there's more than two inductors, it gets more complicated, since you have to take into account the mutual inductance of each of them and how each coils influences the other.
So for 3 coils, there's 3 mutual inductances (<math>M_{12}, M_{13}<math> and <math>M_{23}<math>) and 8 possible equations.
Capacitors
Capacitors follow a different law. The total capacitance of capacitors in series is equal to the reciprocal of the sum of the reciprocals of their individual capacitances:
- <math>{1\over{C_{total}}} = {1\over{C_1}} + {1\over{C_2}} + \cdots + {1\over{C_n}}<math>
Parallel circuits
The voltage is the same across all the components in parallel.
To find the total current, I, use Ohm's Law on each loop, then sum. (See Kirchhoff's circuit laws for an explanation of why this works). Factoring out the voltage (which, again, is the same across all components) gives:
- <math>I_{total} = V \cdot \left(\frac{1} {R_1} + \frac{1} {R_2} + \cdots + \frac{1} {R_n}\right)<math>
Resistors
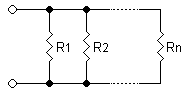
To find the total resistance of all the components, add together the individual reciprocal of each resistance of each component, and take the reciprocal;
- <math>
{1 \over R_{total}} = {1 \over R_{1}} + {1 \over R_{2}} + \cdots + {1 \over R_{n}} <math>
- for components in parallel, having resistances R1, R2, etc.
The above rule can be calculated by using Ohm's law for the whole circuit
- <math>
R_{total} = V / I_{total} <math>
and substituting for Itotal
To find the current in any particular component with resistance Ri, use Ohm's law again.
- <math>
I_i = V / R_i <math>
Note, that the components divide the current according to their reciprocal resistances, so, in the case of two resistors:
- <math>
I_1 / I_2 = R_2 / R_1 <math>
Inductors
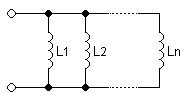
Inductors follow the same law, in that the total inductance of non-coupled inductors in parallel is equal to the reciprocal of the sum of the reciprocals of their individual inductances:
- <math>{1\over{L_{total}}} = {1\over{L_1}} + {1\over{L_2}} + \cdots + {1\over{L_n}}<math>
Once again, this is a little too simplified. Again, one has to take into account mutual inductance. If the mutual inductance between two coils in parallel is M then the equivalent inductor is:
- <math>{1 \over L_{total}} = {1 \over (L_1 + M)} + {1 \over (L_2 + M)}<math> or
- <math>{1 \over L_{total}} = {1 \over (L_1 - M)} + {1 \over (L_2 - M)}<math>
And once again, which formula is the correct one, depends how the magnetic fields of both inductors influence each other.
The principle's the same for more than two inductors, but you now have to take into account the mutual inductance of each inductor on each other inductor and how they influence each other. So for 3 coils, there's 3 mutual inductances (<math>M_{12}, M_{13}<math> and <math>M_{23}<math>) and 8 possible equations.
Capacitors
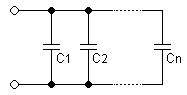
Capacitors follow a different law. The total capacitance of capacitors in parallel is equal to the sum of their individual capacitances:
- <math>C_{total} = C_1 + C_2 + \cdots + C_n<math>
Notation
The parallel property can be represented in equations by two vertical lines "||" (as in geometry) to simplify equations. For two resistors,
- <math> R_{total} = R_1 \| R_2 = {R_1 R_2 \over R_1 + R_2} <math>