Y-delta transform
|
|
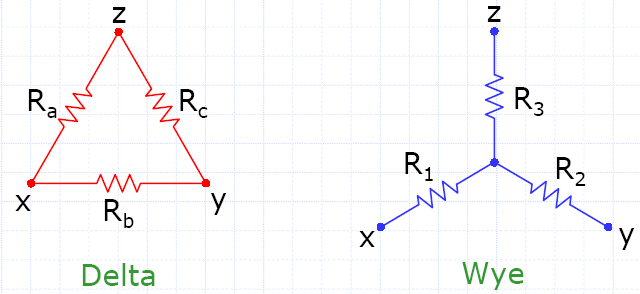
The Y-delta transform (also written Wye-delta transform or Kennelly's Delta-Star transformation) or star-mesh transformation is a mathematical technique to simplify analysis of an electrical network. The name derives from the shapes of the circuit diagrams, which look respectively like the letter Y and the Greek capital letter Δ.
(A Y-delta transformer, on the other hand, is an electrical device that converts Three-phase electric power without a neutral wire into 3-phase power with a neutral wire. It is generally built from 3 independent transformers.)
| Contents |
Basic Y-Delta transformation
The transformation is used to establish equivalence for networks with 3 terminals. Where three elements terminate at one point (node) and none is a source, the node is eliminated by transforming the impedances.
For equivalence, the impedance between any pair of terminals must be the same for both networks.
Transformation equations
- <math>R_1 = \left( \frac{R_aR_b}{R_a + R_b + R_c} \right)<math>
- <math>R_2 = \left( \frac{R_bR_c}{R_a + R_b + R_c} \right)<math>
- <math>R_3 = \left( \frac{R_cR_a}{R_a + R_b + R_c} \right)<math>
Wye-to-Delta transformation equations
- <math>R_a = \left( \frac{R_1R_2 + R_2R_3 + R_3R_1}{R_2} \right)<math>
- <math>R_b = \left( \frac{R_1R_2 + R_2R_3 + R_3R_1}{R_3} \right)<math>
- <math>R_c = \left( \frac{R_1R_2 + R_2R_3 + R_3R_1}{R_1} \right)<math>
Terminology
| United States | United Kingdom |
|---|---|
| Grounded | Earthed |
| Wye or Y | Star |
See also
- Analysis of resistive circuits
- Electrical network: single phase electric power, alternating-current electric power, Three-phase power, polyphase systems for examples of wye and delta connections
- Electric motors for a discussion of wye-delta starting technique
- Lists: List of transforms, List of mathematical topics
References
- William Stevenson, "Elements of Power System Analysis 3rd ed.", McGraw Hill, New York, 1975, ISBN 0070612854fr:théorème de Kennelly