Theodolite
|
|
Optical_Theodolite.jpg
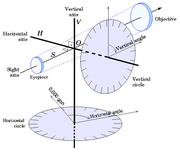
A theodolite (Amer. "transit") is an instrument for measuring both horizontal and vertical angles, as used in triangulation networks. It consists of a telescope mounted movably within two perpendicular axes, the horizontal or trunnion axis, and the vertical axis. These must be mutually perpendicular. The condition where they deviate from perpendicularity (and the amount by which) is referred to as horizontal axis error.
The optical axis of the telescope, called sight axis and defined by the optical center of the objective and the center of the cross-hairs in its focal plane, must similarly be perpendicular to the horizontal axis. If not, we call the deviation from perpendicularity collimation error.
Both axes of a theodolite are equipped with graduated circles that can be read out through microscopes. The vertical circle (the one associated with the horizontal axis!) should read 90° or 100 gon when the sight axis is horizontal (or 270°, 300 gon, when the instrument is in its second position, "turned over"). If not, we call half of the difference with 300 gon index error.
Horizontal axis error, collimation error and index error are regularly determined by calibration, and removed by mechanical adjustment at the factory in case they grow overly large. Their existence is taken into account in the choice of measurement procedure in order to eliminate their effect on the measurement results.
A theodolite is mounted on a tripod by means of a forced centering plate or tribrach, containing three thumbscrews for rapid levelling. Before use, a theodolite must be placed precisely and vertically over the point to be measured -- centering -- and its vertical axis aligned with local gravity -- levelling. The former is done using a plumb, the latter using a spirit level. Fast and accurate procedures for doing both have been developed.
| Contents |
History
The history of theodolites goes back to so-called plane table alhidades, devices allowing the graphical mapping of the terrain. These devices consisted of a plane table and a telescope mounted in a fork-like contraption or alhidade, allowing it to be aimed out of the horizontal plane. The whole assembly rested on a plane table, onto which graphing paper was attached; a ruler connected to the alhidade in such a way as to be always pointing in the same horizontal direction as the telescope, was then used to plot the direction to the target.
The first description of a theodolite, or 'theodelitus', is found in the surveying textbook Pantometria (1571) by Thomas Digges, son of Leonard Digges who is widely credited with the invention. He also invented the name, but its origin is unclear.
Using theodolites in surveying
Triangulation, as invented by Gemma Frisius around 1533, consists of making such direction plots of the surrounding landscape from two separate standpoints. After that, the two graphing papers are superimposed, providing a scale model of the landscape, or rather the targets in it. The true scale can be obtained by just measuring one distance both in the real terrain and in the graphical representation.
Modern triangulation as, e.g., practiced by Snellius, is the same procedure executed by numerical means. Photogrammetric block adjustment of stereo pairs of aerial photographs is a modern, three-dimensional variant.
In the late 1780s Jesse Ramsden, a Yorkshireman from Halifax, England who had developed the technique of dividing angular scales accurately to within a second of arc, was commissioned to build a new instrument for the British Ordnance Survey. The Ramsden theodolite was used over the next few years to map the whole of southern Britain by triangulation.
In network measurement, the use of forced centering speeds up operations while maintaining the highest precision. The theodolite or the target can be rapidly removed from, or socketed into, the forced centering plate with sub-mm precision. Nowadays GPS antennas used for geodetic positioning use a similar mounting system. The height of the reference point of the theodolite -- or the target -- above the ground bench mark must be measured precisely.
Modern theodolites
In today's theodolites, the reading out of the horizontal and vertical circles is usually done electronically. The readout is done by a rotary encoder, which can be absolute, e.g., using Gray codes, or incremental, using equidistant light and dark radial bands. In the latter case the circles spin rapidly, reducing angle measurement to electronic measurement of time differences. Additionally, lately CCD sensors have been added to the focal plane of the telescope allowing both auto-targeting and the automated measurement of residual target offset. All this is implemented in embedded software.
Today's theodolites are usually equipped with integrated electro-optical distance measuring devices, allowing the measurement in one go of complete three-dimensional vectors -- albeit in instrument-defined polar co-ordinates -- which can then be transformed to a pre-existing co-ordinate system in the area by means of a sufficient number of control points. The technique is called free station position surveying and is widely used in mapping surveying. The instruments, "intelligent" theodolites called self-registering tachometers or "total stations", perform the necessary operations, saving data into internal registering units, or into external data storage devices. Typically, ruggedized laptops or PDAs are used for this purpose.
See also
fa:دوربین مهندسی fr:Théodolite nl:Theodoliet ja:トランシット pl:Teodolit