Tetragonal
|
|
In crystallography, the tetragonal crystal system is one of the 7 lattice point groups. Tetragonal lattices result from stretching a cubic lattice along one of its lattice vectors, so that the cube becomes a rectangular prism with a square base (a by a) and height (c, which is different from a).
There are two tetragonal Bravais lattices: the simple tetragonal (from stretching the simple-cubic lattice) and the centered tetragonal (from stretching either the face-centered or the body-centered cubic lattice).
| simple tetragonal | body-centered tetragonal |
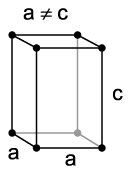
| 
|
The point groups that fall under this crystal system are listed below, followed by their representations in international notation and Schoenflies notation, and mineral examples.
| name | international | Schoenflies | example |
| ditetragonal bipyramidal | <math>\frac4m \frac2m \frac2m<math> | D4h | rutile |
| ditetragonal pyramidal | <math>4mm<math> | C4v | |
| tetragonal bipyramidal | <math>\frac4m<math> | C4h | |
| tetragonal pyramidal | 4 | C4 | wulfenite |
| ditetragonal alternating | <math>\overline{4}2m<math> | D2d | chalcopyrite |
| tetragonal trapezohedral | 422 | D4 | phosgenite |
| tetragonal alternating | <math>\overline{4}<math> | S4 |
