Pati-Salam model
|
|
The Pati-Salam model is a GUT theory which states that the gauge group is either SU(4)× SU(2)L× SU(2)R or ( SU(4)× SU(2)L× SU(2)R )/Z2 and the fermions form three families, each consisting of the representations (4,2,1) and <math>(\bar 4,1,2)<math>. This needs some explanation. The center of SU(4)× SU(2)L× SU(2)R is Z4× Z2L× Z2R. The Z2 in the quotient refers to the two element subgroup generated by the element of the center corresponding to the 2 element of Z4 and the 1 elements of Z2L and Z2R. This includes the right handed neutrino, which is now likely believed to exist. See neutrino oscillations. There is also a (4,1,2) and/or a <math>(\bar 4,1,2)<math> scalar field called the Higgs field which acquires a VEV. This results in a spontaneous symmetry breaking from <math>SU(4)\times SU(2)_L\times SU(2)_R<math> to <math>[SU(3)\times SU(2)\times U(1)]/\mathbb{Z}_3<math> or from <math>[SU(4)\times SU(2)_L\times SU(2)_R]/\mathbb{Z}_2<math> to <math>[SU(3)\times SU(2)\times U(1)]/\mathbb{Z}_6<math> and also, <math>(4,2,1)\rightarrow (3,2)_{\frac{1}{6}}\oplus (1,2)_{-\frac{1}{2}}<math>, <math>(\bar{4},1,2)\rightarrow (\bar{3},1)_{\frac{1}{3}}\oplus (\bar{3},1)_{-\frac{2}{3}}\oplus (1,1)_1\oplus (1,1)_0<math>, <math>(6,1,1)\rightarrow (3,1)_{-\frac{1}{3}}\oplus (\bar{3},1)_{\frac{1}{3}}<math>, <math>(1,3,1)\rightarrow (1,3)_0<math> and <math>(1,1,3)\rightarrow (1,1)_1\oplus (1,1)_0\oplus (1,1)_{-1}<math>. See restricted representation. Of course, calling the representations things like <math>(\bar{4},1,2)<math> and (6,1,1) is purely a physicist's convention, not a mathematician's convention, where representations are either labelled by Young tableaux or Dynkin diagrams with numbers on their vertices, but still, it is standard among GUT theorists.
Actually, it is possible to extend the Pati-Salam group so that it has two connected components. The relevant group is now the semidirect product <math>\{[SU(4)\times SU(2)_L\times SU(2)_R]/\mathbb{Z}_2\}<math>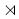 <math>\mathbb{Z}_2<math>. The last Z2 also needs explaining. It corresponds to an automorphism of the (unextended) Pati-Salam group which is the composition of an involutive outer automorphism of SU(4) which isn't an inner automorphism with interchanging the left and right copies of SU(2). This explains the name left and right and is one of the main motivations for originally studying this model. This extra "left-right symmetry" restores the concept of parity which had been shown not to hold at low energy scales for the weak interaction. In this extended model, <math>(4,2,1)\oplus(\bar{4},1,2)<math> is an irrep and so is <math>(4,1,2)\oplus(\bar{4},2,1)<math>. This is the simplest extension of the minimal left-right model unifying QCD with B-L.
<math>\mathbb{Z}_2<math>. The last Z2 also needs explaining. It corresponds to an automorphism of the (unextended) Pati-Salam group which is the composition of an involutive outer automorphism of SU(4) which isn't an inner automorphism with interchanging the left and right copies of SU(2). This explains the name left and right and is one of the main motivations for originally studying this model. This extra "left-right symmetry" restores the concept of parity which had been shown not to hold at low energy scales for the weak interaction. In this extended model, <math>(4,2,1)\oplus(\bar{4},1,2)<math> is an irrep and so is <math>(4,1,2)\oplus(\bar{4},2,1)<math>. This is the simplest extension of the minimal left-right model unifying QCD with B-L.
Since the homotopy group <math>\pi_2\left(\frac{SU(4)\times SU(2)}{[SU(3)\times U(1)]/\mathbb{Z}_3}\right)=\mathbb{Z}<math>, this model predicts monopoles. See 't Hooft-Polyakov monopole.
This model was invented by Jogesh Pati and Abdus Salam.
