Fabry-Perot interferometer

In optics, a Fabry-Perot interferometer or etalon is typically made of a transparent plate with two reflecting surfaces, or two parallel highly-reflecting mirrors. (Technically the former is an etalon and the latter is an interferometer, but the terminology is often used inconsistently.) Its transmission spectrum as a function of wavelength exhibits peaks of large transmission corresponding to resonances of the etalon.

It is named after Charles Fabry and Alfred Pérot.

The most frequent industrial use of etalons is in data transmission. They are used as optical filters in fiberoptic modems that use wavelength division multiplexing. Normally such equipment mounts banks of miniature tuned fused silica or diamond etalons.

A typical fiberoptic etalon is a small iridescent cube about 2mm on a side, mounted in a small high-precision rack. The materials are chosen to maintain stable mirror-to-mirror distances, and thus keep stable frequencies under high temperatures. Diamond is preferred because it has greater heat transmission and still has a low coefficient of expansion.

A recent (2005) innovation is to make solid etalons that are themselves optic fibers. This eliminates most mounting, alignment and cooling difficulties.

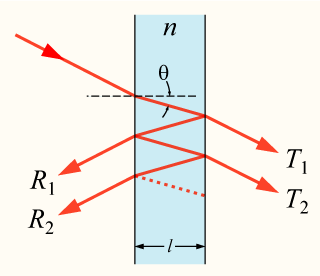
The varying transmission function of an etalon is caused by interference between the multiple reflections of light between the two reflecting surfaces. Constructive interference occurs if the transmitted beams are in phase, and this corresponds to a high-transmission peak of the etalon. If the transmitted beams are out-of-phase, destructive interference occurs and this corresponds to a transmission minimum. Whether the multiply-reflected beams are in-phase or not depends on the wavelength (λ) of the light, the angle the light travels through the etalon (θ), the thickness of the etalon (l) and the refractive index of the material between the reflecting surfaces (n).

The phase difference between each succeeding reflection is given by δ:

<math>\delta = \left( \frac{2 \pi}{\lambda} \right) 2 n l \cos\theta, <math>

the term 2nl cos θ is equal to the optical path length of a double traversal of the etalon plate.

If both surfaces have a reflection coefficient R, the transmission function of the etalon is given by:

<math>T_e = \left[ 1 + \frac{4R}{ (1-R)^2} \sin^2 \left( \frac{\delta}{2} \right) \right]^{-1} <math>

Maximum transmission (T_e = 1) occurs when the optical path-length difference (2nl cos θ) between each transmitted beam is an integer multiple of the wavelength. In the absence of absorption, the reflectivity of the etalon R_e is the complement of the transmission, such that T_e + R_e = 1. The maximum reflectivity is given by:

<math>R_{max} = \frac {4R}{(1+R)^2} <math>

and this occurs when the path-length difference is equal to half an odd multiple of the wavelength.

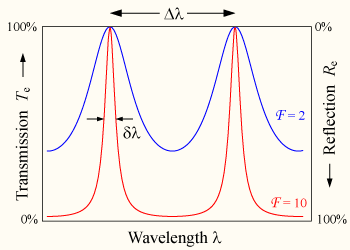
The wavelength separation between adjacent transmission peaks is called the free spectral range (FSR) of the etalon, Δλ, and is given by:

<math>\Delta\lambda = \frac{ \lambda_0^2}{2nl \cos\theta } <math>

where λ₀ is the central wavelength of the nearest transmission peak. The FSR is related to the full-width half-maximum, δλ of any one transmission band by a quantity known as the finesse:

<math> \mathcal{F} = \frac{\Delta\lambda}{\delta\lambda} \approx \frac{\pi R^{1/2} }{(1-R)} <math>

with the approximation being valid for R>0.5. Etalons with high finesse show sharper transmission peaks with lower minimum transmission coefficients.

A Fabry-Perot interferometer differs from a Fabry-Perot etalon in the fact that the distance l between the plates can be tuned in order to change the wavelengths at which transmission peaks occur. Due to the angle dependence of the transmission, the peaks can also be shifted by rotating the etalon with respect to the beam.

Fabry-Perot interferometers or etalons are used in optical modems, spectroscopy, lasers, and astronomy.

A related device is the Gires-Tournois etalon.

See also

• Dichroic filter
• Dichroic prismde:Fabry-Pérot-Interferometer