Examples of differential equations
|
|
| Contents |
A separable first order ordinary differential equation
A separable ordinary differential equation of the first order has the general form:
- <math>\frac{dy}{dt} + f(t) y = 0,<math>
where f(t) is some known function. We may solve this by separation of variables (moving the y terms to one side and the t terms to the other side),
- <math>\frac{dy}{y} = -f(t)\, dt.<math>
Integrating, we find
- <math>\ln y = -F(t) + C\,<math>
where
- <math>F(t) = \int f(t)\,dt<math>
is the antiderivative of f(t) and C is a constant. Then, by exponentiation, we obtain
- <math>y = A e^{-F(t)},\,<math>
with A an arbitrary constant. (We can easily confirm that this is a solution by plugging it into the original differential equation.)
Some elaboration is needed since f(t) is not in fact a constant, indeed it might not even be integrable. Arguably, one must also assume something about the domains of the functions involved before the equation is fully defined. Are we talking complex functions, or just real, for example? The usual textbook approach is to discuss forming the equations well before considering how to solve them.
Non-separable first order linear ordinary differential equations
Some first order linear ODEs (ordinary differential equations) are not separable like in the above example. In order to solve non-separable first order linear ODEs one must use what is known as an integrating factor. This technique will be shown below.
Consider first order linear ODEs of the general form:
<math>\frac{dy}{dx} + p(x)y = q(x)<math>
The method for solving this equation relies on a special "integrating factor", μ:
<math>\mu = e^{\int_{}^{} p(x)\, dx}<math>
Multiply both sides of the differential equation by μ to get:
<math>\mu{\frac{dy}{dx}} + \mu{p(x)y} = \mu{q(x)}<math>
Because of the special μ we picked, this simplifies to:
<math>\mu{\frac{dy}{dx}} + y{\frac{d{\mu}}{dx}} = \mu{q(x)}<math>
Using the product rule we get:
<math>\frac{d}{dx}{(\mu{y})} = \mu{q(x)}<math>
Integrating both sides we get:
<math>\mu{y} = \left(\int\mu q(x)\, dx\right) + C<math>
Finally, to solve for <math>y<math> we divide both sides by <math>\mu<math>:
<math>y = \frac{\left(\int\mu q(x)\, dx\right) + C}{\mu}<math>
(Since μ is a function of x, we cannot simplify any more.)
A simple mathematical model
Suppose a mass is attached to a spring, which exerts an attractive force on the mass proportional to the extension/compression of the spring and ignore any other forces (gravity, friction etc). We shall write the extension of the spring at a time <math>t<math> as <math>x(t)<math>. Now, using Newton's second law we can write (using convenient units)
- <math>\frac{d^2x}{dt^2} = - x<math>
If we look for solutions that have the form <math>C e^{kt}<math>, where <math>C<math> is a constant, we discover the relationship <math>k^2 + 1 = 0<math>, and thus <math>k<math> must be one of the complex numbers <math>i<math> or <math>-i<math>. Thus, using Euler's theorem we can say that the solution must be of the form:
- <math>x(t) = A \cos t + B \sin t<math>
To fix the unknown constants <math>A<math> and <math>B<math>, we need initial conditions, i.e. to specify the state of the system at a given time (usually taken to be <math>t = 0<math>).
For example, if we suppose at <math>t = 0<math> the extension is a unit distance (<math>x = 1<math>), and the particle is not moving (<math>dx/dt = 0<math>). We have
- <math>x(0) = A \cos 0 + B \sin 0 = A = 1,<math>
and so <math>A = 1<math>.
- <math>x'(0) = -A \sin 0 + B \cos 0 = B = 0,<math>
and so <math>B = 0<math>.
Therefore <math>x(t) = \cos t<math>. (This is an example of simple harmonic motion.)
Improving our model
The above model of an oscillating mass on a spring is plausible but not really realistic. For a start, we've invented a perpetual motion machine which violates the second law of thermodynamics. So lets consider adding some friction for realism. Now, experimental scientists will tell us that friction will tend to decelerate the mass and have magnitude proportional to its velocity (i.e. <math>dx/dt<math>). Our new differential equation, expressing the balancing of the acceleration and the forces, is
- <math>\frac{d^2x}{dt^2} = - c \frac{dx}{dt} - x<math>
where <math>c<math> is our coefficient of friction, and <math>c > 0<math>. Again looking for solutions of the form <math>A e^{kt}<math>, we find that
- <math>k^2 + c k + 1 = 0.<math>
This is a quadratic equation which we can solve. If <math>c < 2<math> we have complex roots <math>a \pm i b<math>, and the solution (with the above boundary conditions) will look like this:
- <math>x(t) = e^{at} \left(\cos bt - \frac{a}{b} \sin bt \right) <math>
(We can show that <math>a < 0<math>)
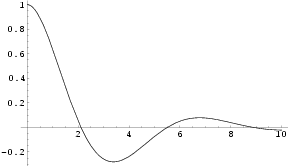
This is a damped oscillator, and the plot of displacement against time would look something like this:
which does resemble how we'd expect a vibrating spring to behave as friction removed the energy from the system.
A simple exact equation
An exact differential equation is a first-order ordinary differential equation of implicit form
- <math>I(x, y)\, dx + J(x, y)\, dy = 0, \,\!<math>
such that
- <math>\frac{\partial I}{\partial y}(x, y) = \frac{\partial J}{\partial x}(x, y).<math>
This equation has the solution
- <math>\int_{x_0}^{x} I(u, y)\, du + \int_{y_0}^{y} J_\partial (v)\, dv = 0<math>
where
- <math>J_\partial (y) = J(x, y) - \frac{\partial}{\partial y} \int_{x_0}^{x} I(u, y)\, du,<math>
u and v being dummy variables; x0 and y0 being initial-value constants.
See also
Bibliography
- A. D. Polyanin and V. F. Zaitsev, Handbook of Exact Solutions for Ordinary Differential Equations, 2nd Edition, Chapman & Hall/CRC Press, Boca Raton, 2003; ISBN 1584882972.
External link
- Ordinary Differential Equations (http://eqworld.ipmnet.ru/en/solutions/ode.htm) at EqWorld: The World of Mathematical Equations.