Einstein-Cartan theory
|
|
Einstein-Cartan theory in theoretical physics extends general relativity, to handle spin angular momentum correctly. As the master theory of classical physics, general relativity has one known flaw: it cannot describe exchange of intrinsic angular momentum (spin) and orbital angular momentum. There is a qualitative theoretical proof showing that general relativity must be extended to Einstein-Cartan theory when matter with spin is present. Experimental effects are too small to be observed at the present time.
The problem is rooted in the Riemannian geometry (on which general relativity is based), in which the Ricci curvature tensor
- Rab
and therefore the Einstein curvature tensor Gab
- Rab - 1/2 Rgab
must be symmetric in a and b (that is, Rab = Rba). In general relativity, the Einstein curvature tensor models local gravitational forces, and it is equal (up to a gravitational constant) to the energy-momentum tensor
- Tab
The symmetry of the Einstein curvature tensor forces the momentum tensor to be symmetric. However, when spin and orbital angular momentum are being exchanged, the momentum tensor is known to be nonsymmetric according to the general equation of conservation of angular momentum
- divergence of spin current − ½(Tab − Tba) = 0.
Therefore general relativity cannot properly model spin-orbit coupling.
In 1922 Elie Cartan conjectured that general relativity should be extended by including affine torsion, which allows the Ricci tensor to be non-symmetric. Although spin-orbit coupling is a relatively minor phenomenon in gravitational physics, Einstein-Cartan theory is quite important because it makes clear that an affine theory, not a metric theory, provides a better description of gravitation. The extension of Riemannian geometry to include affine torsion is now known as Riemann-Cartan geometry.
| Contents |
Introduction
The basic mathematics underlying spacetime physics is affine differential geometry, in which we endow an n dimensional differentiable manifold M with a law of parallel translation of vectors along paths in M. (At each point of a differentiable manifold, we have a linear space of tangent vectors, but we have no way to transport vectors to another point, or to compare vectors at two points in M.) The parallel translation preserves linear relationships between vectors; that is, if two vectors u and v at the same point of M parallel translate along a curve to vectors u' and v', then
- a u + b v
parallel translates to a
- a u' + b v'.
Parallelism in affine differential geometry is path-dependent; that is, if you parallel translate a vector along two different paths with the same starting and ending points, the resulting vectors at the end point in general differ. The difference between parallel-translating a vector along different curves is the essential meaning of curvature, which is the central concept in differential geometry.
(In the more abstract language of fiber bundles, the law of parallel translation is called a connection, which can be defined by a connection form on the principal frame bundle of M, or as a connection form on the tangent bundle of M. The structure group of the principal frame bundle is the general linear group GL(n,R).)
In (pseudo) Riemannian geometry, an n dimensional differential manifold M is endowed with a Riemannian metric g, which is a nondegenerate linear map mapping two tangent vectors to a real number. The metric uniquely determines a law of parallel translation that preserves inner products between vectors and has zero torsion. This law of parallel translation is called the Levi-Civita connection.
(In the more abstract language of fiber bundles, if the metric g is preserved by the connection, the structure group of the principal bundle is reducible to the orthogonal group SO(p,q), where the metric g has p principal directions with positive length and q principal directions with negative length.)
A Riemann-Cartan geometry is uniquely determined by
1) a metric tensor field g which specifies all lengths of vectors and angles between vectors.
2) the requirement that lengths and angles are preserved by parallel transport. This is expressed by the condition that the covariant derivative of the metric tensor vanishes.
<math>\nabla \bold{g}=0<math>
where ∇ is the covariant derivative determined by the affine connection.
3) an affine torsion field Θ
<math>\nabla_\bold{u}\bold{v}-\nabla_{\bold{v}}\bold{u}-[\bold{u},\bold{v}]=\Theta(\bold{u},\bold
{v})<math>
where u and v are vector fields and [,] is the Lie bracket. (See Lie algebra for the definition of Lie bracket.)
In Riemann-Cartan geometry, the curvature tensor has a rotational part R(k,l,j,^i], analogous to the curvature in Riemannian geometry, and a translational part, the affine torsion T[i,j,^k]. The rotational curvature R(k,l,j,^i] describes the rotation in the i,j plane experienced by a vector that is parallel translated around a small loop in the k,l plane in the base manifold. The translational curvature T[k,l,^i] describes the translation in the i direction resulting from 'developing' into X a small loop in the base manifold X.
A Riemann-Cartan geometry with zero torsion is a Riemannian geometry.
The best way to formulate Einstein-Cartan is to distinguish between tangents to the spacetime M and tangents to an associated affine fiber space, X. X is a (pseudo-) Euclidean space (a Minkowski space) with metric g and no origin, so you cannot add two points in X or multiply a point in X by a scalar. The affine connection tells us how to parallel translate points in X and tangents to X along curves in M, not how to parallel translate tangents to M. The translational part of the affine connection acts like an (inverse) frame field that enables us to identify tangents to M with tangents to X, and pulls back the metric g on X to a metric on M. While at first the distinction between tangents to M and tangents to X may seem artificial, the equations of Einstein-Cartan theory make it clear that conserved currents (like momentum and spin) are represented by tangents to X, which are parallel translated by the connection, while directions in M (and flux boxes through which conserved currents flow) are represented by tangents to M, which never need to be parallel translated along a curve in M. In this article, we use Roman indices i,j,k,... to denote tangent vectors to M and Roman indices a,b,c,... to denote tangents to the fiber space X. For example the momentum tensor P[a,^k] represents the flux normal to the spacetime k-direction of momentum in the a-direction, and the spin tensor Spin[a,b,^k] represents the flux normal to the spacetime k-direction of spin in the a,b plane.
(Advanced point: In order to accommodate spinor fields, all of the constructions of Riemannian and Riemann-Cartan geometry can be generalized from orthogonal groups, principal orthogonal frame bundles and associated tangent bundles to spin groups, principal spin bundles and associated spinor bundles. A spacetime manifold admits a spin bundle over its principal frame bundle only if the second Stiefel-Whitney class of M is zero. The Riemann tensor is the curvature form for (generalized to include boosts) rotations (i.e. the spin(p,q) part) while torsion is the curvature form for translations (R4.)
A geometric interpretation of affine torsion comes from continuum mechanics of solid materials. Affine torsion is the continuum approximation to the density of dislocations that are studied in metallurgy and crystallography. The simplest kinds of dislocations in real crystals are
- edge dislocations (formed by adding an extra half-plane of atoms to a perfect crystal, so you get a defect in the regular crystal structure along the line where the extra half-plane ends), and
- screw dislocations (formed by inserting a "parking garage ramp" that extends to the edges of the garage into an otherwise perfectly layered structure).
We can think of a Riemann-Cartan geometry as uniquely determined by the lengths and angles of vectors and the density of dislocations in the affine structure of the space.
General relativity set the affine torsion to zero, because it did not appear necessary to provide a model of gravitation (with a consistent set of equations that led to a well-defined initial value problem).
Derivation of field equations of Einstein-Cartan theory
General relativity and Einstein-Cartan theory both use the scalar curvature as Lagrangian. General relativity obtains its field equations by varying the Einstein-Hilbert action (integral of the Lagrangian over spacetime) with respect to the metric tensor. The result is the famous Einstein equations:
- <math>R_{ab}-\frac{1}{2}R g_{ab}=\frac{8 \pi G}{c^4}T_{ab}<math>
where
- <math>R_{ab}<math> are the Ricci tensor components (a contraction of the full Riemann curvature tensor with four indices).
- <math>g_{ab}<math> are the (symmetric nondegenerate) metric tensor components.
- <math>R<math>is the scalar curvature (Ricci scalar).
- <math>T_{ab}<math> are the energy-momentum tensor components.
- <math>G<math> is the Newtonian gravitational constant.
- <math>c<math> is the speed of light.
The contracted second Bianchi identity of Riemannian geometry becomes, in general relativity,
- <math>div T = T^{ab}{}_{;b}=0<math>
which makes conservation of energy and momentum equivalent to an identity of Riemannian geometry.
A basic question in formulating Einstein-Cartan theory is which variables in the action to vary to get the field equations. You can vary the metric tensor g[i,j] and the torsion tensor T[i,j,^k]. However, this makes the equations of Einstein-Cartan theory messier than necessary and disguises the geometric content of the theory. The key insight is to let the symmetry group of Einstein-Cartan theory be the inhomogeneous rotation group (which includes translations in space and time), that is, the analogue of the Euclidean group. (The inhomogeneous rotational symmetry is broken by the fact that the zero point in each tangent fiber is still a preferred point, as in ordinary Riemannian geometry based on the homogeneous rotation group.) We vary the action with respect to the affine connection coefficients associated with translational and rotational symmetries. (A similar approach in general relativity is called Palatini variation, in which the action is varied with respect to the rotational connection coefficients instead of the metric; general relativity has no translational connection coefficients.)
The resulting field equations of Einstein-Cartan theory are:
- R{a,k} - 1/2 g{a,k} R = 8 π K/c^2 P{a,k}
- S{a,b,^k} = 8 π K/c^2 Spin{a,b,^k}
where
- Spin{a,b,^k} is the spin tensor of all matter and radiation
- S{a,b,^k} is the modified torsion tensor equal to
T{a,b,^k} + g{a,^k} T{b,m,^m} – g{b,^k} T{a,m,^m}.
- T{a,b,^k} is the affine torsion tensor.
The first equation is the same as in general relativity, except that the affine torsion is included in all the curvature terms, so P{a,j} need not be symmetric.
The contracted second Bianchi identity of Riemann-Cartan geometry becomes, in Einstein-Cartan theory,
- div(P)= some very small terms that are products of curvature and torsion,
- div(Spin) = - antisymmetric part of P{a,j}.
The conservation of momentum is altered by products of gravitational field strength and spin density. These terms are exceedingly small under normal conditions, and they seem reasonable in that the gravitational field itself carries energy. The second equation is conservation of angular momentum, in a form that accommodates spin-orbit coupling.
Geometric insights from Einstein-Cartan theory
First geometric insight
Spin (intrinsic angular momentum) consists of dislocations in the fabric of spacetime. For ordinary fermions (particles with spin such as protons, neutrons and electrons), these are screw dislocations (parking garage ramps) with timelike direction of the screw. That is, for a particle with spin in the +z direction, traversing a space-like loop in the x-y plane around the particle parallel translates you into the past or the future by a small amount.
Second geometric insight
It has long been known that the spin angular momentum tensor Spin(a,b,^k} is the "Noether current" of rotational symmetry of spacetime, and the momentum tensor P{a,k} is the Noether current of translational symmetry. (The Noether theorem states that, for every symmetry of a physical system, there is a corresponding conserved current derived by performing the symmetry transformation on the Lagrangian.) Einstein-Cartan theory provides a clean derivation of momentum as the Noether current of translational symmetry. It may be that general relativity without rotational connection coefficients (which would have introduced affine torsion to the theory) cannot provide a clean derivation of the momentum as the Noether current of translational symmetry.
To put it in other words, since we have a diffeomorphism covariant theory, picking out spatial translations and rotations out of all the diffeomorphisms is completely arbitrary. However, as a R4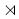
spin(3,1) theory, we can perform a R4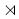spin(3,1) gauge transformation on the fibers. Note that both transformations are completely different in principle. That's why they give rise to different Noether currents.
Third geometric insight
In Einstein-Cartan theory, we should distinguish between tensor indices that represent conserved currents (like momentum and spin) and indices that represent spacetime boxes (through which fluxes of the currents are measured). (This is similar to other gauge theories, like electromagnetism and Yang-Mills theory, where we would never confuse spacetime indices that represent flux boxes with the fiber indices that represent the conserved currents.)
Writing Einstein-Cartan theory in the simplest form requires distinguishing two kinds of tensor indices:
- (1) directions in the idealized Minkowski "fiber space" at each point of spacetime (the space of tangent vectors).
- (2) tangents to the spacetime manifold that describe flux boxes, and
These two types of indices have two roles in the theory.
- (1) The conserved currents are represented by the fiber indices.
- (2) All the derivative indices in Einstein-Cartan theory are spacetime indices. Furthermore, the derivatives are all 'exterior derivatives,' which measure fluxes of currents through spacetime boxes (or divergences, which are exterior derivatives disguised by "Hodge dual" operations). The derivative indices are spacetime indices, as are all the indices with which they are antisymmetrized in the exterior derivatives (or the indices with which the derivative indices are contracted in the case of divergences).
In more geometric terms, we have TWO distinct vector bundles, TM (the tangent bundle with the fibers being tangent spaces with structure group GL(4,R)) and T (the "Minkowski" vector bundle with the fibers being "Minkowski spaces with a fixed origin" with structure group R4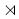Spin(3,1)). The duals of these two vector bundles are T*M (the cotangent bundle) and T*. A general tensor field would be a global section of the fiber product of copies of these four vector bundles.
The statement that all derivatives are covariant exterior derivatives (and covariant Lie derivatives too by the way) boils down to the fact that the affine connection in this formalism is a connection for V and T, not TM and in fact, we don't have ANY independent connection for TM.
For example, in the field equations of Einstein-Cartan theory stated above, we should interpret the indices a,b as fiber indices and the indices i,j as base space indices. The momentum tensor P{a,^k} describe the flux of a-momentum through a flux box normal to the k-direction in spacetime, and the spin tensor Spin{a,b,^k} describes the flux of angular momentum in the a × b plane through a flux box normal to the k-direction in spacetime.
(Before the distinction between these types of indices became clear, researchers would vary the action with respect to the metric to get what they called the "momentum tensor" (the 'wrong' one) and also sometimes vary with respect to the translational connection coefficients and get a different momentum tensor (the 'right' one) and they did not know which one was the real momentum tensor. The equations of the theory had many unnecessary terms because they did not distinguish between the base space and fiber space tensor indices.)
Fourth geometric insight
Einstein-Cartan theory is about defects in the affine (Euclidean-like but curved) structure of spacetime; it is not a metric theory of gravitation.
We have seen above that the affine torsion is a continuum model of dislocation density. The full rotational (or Riemannian) curvature tensor
- Ra,b,i,j
also has an interpretation as a density of defects in continuum mechanics. It is the continuum model of a density of "disclination defects." A disclination results when you make a cut into a continuum (imaging making a radial cut from the edge to the center of a disk of rubber) and insert (or excise) an angular wedge of material, so that the sum of the angles surrounding the endpoint of the cut is more tha (or less than) 2π radians. (Indeed, this procedure can convert a flat disk into a bowl: make many small radial cuts from the edge with varying lengths part-way to the center, excise wedges of material of the appropriate angular width, and sew up the cuts.)
The central role of affine defects explains why the clean way to do Einstein-Cartan theory is to vary the translational and rotational connection coefficients (not the metric) and to distinguish between the base space and fiber indices. The connection coefficients are keeping track of the dislocation and disclination defects in the affine structure of spacetime. It is as if spacetime were composed of many microcrystals of perfectly flat Minkowski space, and these perfect micro-pieces are fit together with defects like dislocations and disclinations.
The central role of the translational and rotational connection coefficients as field variables is recognized in modern efforts to quantize general relativity under the name "Ashtekar variables." The Ashtekar variables are essentially the translational and rotational connection coefficients, suitably worked into a Hamiltonian formulation of general relativity.
General relativity plus matter with spin implies Einstein-Cartan theory
For decades, it was thought that Einstein-Cartan theory is based on an independent assumption to include affine torsion. Since the effect of torsion is too small to measure empirically so far, Einstein-Cartan theory was considered one of many speculative (and largely ignored) extensions of general relativity.
It has been shown that general relativity plus a fluid of many tiny rotating black holes generate affine torsion and essentially the equations of Einstein-Cartan theory. The "proof" uses a standard Kerr-Newman rotating black hole solution of general relativity. It computes the non-zero time-like translation that occurs when you parallel-translate an affine frame (keeping track of translation as well as rotation) around an equatorial loop near the black hole. The word "proof" appears in quotes because, while it is intuitively compelling that this implies Einstein-Cartan theory, the proof of convergence to the equations of Einstein-Cartan theory has not been done.
References
1. Cartan, E., Comptes Rendus 174, (1922), 437-439, 593-595, 734-737, 857-860, 1104-1107.
2. Kibble, T. W. B., J. Math. Phys., 2, (1961) 212.
3. Hehl, F. W., Gen. Rel. Grav., 4 (1973), 333; 5 (1974), 491.
4. Kerlick, G. D. (1975). thesis, Department of Physics, Princeton U.
5. Petti, R.J., Gen. Rel. Grav. 7 (1976), 869-883.
6. Petti, R. J., Gen. Rel. Grav. 18 (1986), 441-460.
7. Kleinert, H. (1987). In "Gauge Fields in Condensed Matter" (World Scientific Publishing). See especially “Part IV: Differential Geometry of Defects and Gravity with Torsion.”
8. Kleinert, H., Gen. Rel. Grav. 32 (2000), 769. r 9. Gronwald, F. and Hehl, F. W. (1996). In On the Gauge Aspects of Gravity
10. Petti, R. J., Gen. Rel. Grav. 33 (2001), 209-217.
11. Saa, Alberto Einstein-Cartan theory of gravity revisited, gr-qc/9309027
External link
- For reference 9 above: [1] (http://arXiv.org/archive/gr-qc/9602013).es:Teoría de Einstein-Cartan