E6 (mathematics)
|
|
In mathematics, E6 is the name of a Lie group and also its Lie algebra <math>\mathfrak{e}_6<math>. It is one of the five exceptional simple Lie groups as well as one of the simply laced groups. E6 has rank 6 and dimension 78. Its center is the cyclic group Z3. Its outer automorphism group is the cyclic group Z2. Its fundamental representation is 27-dimensional (complex) and its dual representation, which is inequivalent to it is also 27-dimensional.
In particle physics, E6 plays a role in some grand unified theories.
| Contents [hide] |
Algebra
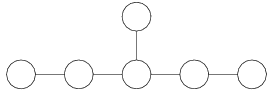
Dynkin diagram
Roots of E6
Although they span a six-dimensional space, it's much more symmetrical to consider them as vectors in a six-dimensional subspace of a nine-dimensional space.
- (1,-1,0;0,0,0;0,0,0), (-1,1,0;0,0,0;0,0,0),
- (-1,0,1;0,0,0;0,0,0), (1,0,-1;0,0,0;0,0,0),
- (0,1,-1;0,0,0;0,0,0), (0,-1,1;0,0,0;0,0,0),
- (0,0,0;1,-1,0;0,0,0), (0,0,0;-1,1,0;0,0,0),
- (0,0,0;-1,0,1;0,0,0), (0,0,0;1,0,-1;0,0,0),
- (0,0,0;0,1,-1;0,0,0), (0,0,0;0,-1,1;0,0,0),
- (0,0,0;0,0,0;1,-1,0), (0,0,0;0,0,0;-1,1,0),
- (0,0,0;0,0,0;-1,0,1), (0,0,0;0,0,0;1,0,-1),
- (0,0,0;0,0,0;0,1,-1), (0,0,0;0,0,0;0,-1,1),
All 27 combinations of <math>(\bold{3};\bold{3};\bold{3})<math> where <math>\bold{3}<math> is one of <math>(\frac{2}{3},-\frac{1}{3},-\frac{1}{3})<math>, <math>(-\frac{1}{3},\frac{2}{3},-\frac{1}{3})<math>, <math>(-\frac{1}{3},-\frac{1}{3},\frac{2}{3})<math>
All 27 combinations of <math>(\bold{\bar{3}};\bold{\bar{3}};\bold{\bar{3}})<math> where <math>\bold{\bar{3}}<math> is one of <math>(-\frac{2}{3},\frac{1}{3},\frac{1}{3})<math>, <math>(\frac{1}{3},-\frac{2}{3},\frac{1}{3})<math>, <math>(\frac{1}{3},\frac{1}{3},-\frac{2}{3})<math>
Simple roots
- (0,0,0;0,0,0;0,1,-1)
- (0,0,0;0,0,0;1,-1,0)
- (0,0,0;0,1,-1;0,0,0)
- (0,0,0;1,-1,0;0,0,0)
- (0,1,-1;0,0,0;0,0,0)
- <math>(\frac{1}{3},-\frac{2}{3},\frac{1}{3};-\frac{2}{3},\frac{1}{3},\frac{1}{3};-\frac{2}{3},\frac{1}{3},\frac{1}{3})<math>
Weyl/Coxeter group
Its Weyl/Coxeter group is symmetry group of the E6 polytope.
Cartan matrix
- <math>
\begin{pmatrix} 2&-1&0&0&0&0\\ -1&2&-1&0&0&0\\ 0&-1&2&-1&-1&0\\ 0&0&-1&2&0&0\\ 0&0&-1&0&2&-1\\ 0&0&0&0&-1&2 \end{pmatrix} <math>
| E6 | E7 | E8 | F4 | G2 |