Conway's Game of Life
|
|
The Game of Life is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is the best-known example of a cellular automaton.
| Contents |
Origins
Conway became interested in a problem in group theory proposed by mathematician John Leech having to do with the symmetry group of a particular dense packing of spheres in 24 dimensions. Conway found some remarkable properties and published the results in 1968. Conway was also interested in a problem presented in the 1940s by renowned mathematician John von Neumann. Von Neumann tried to find a hypothetical machine that could build copies of itself and succeeded when he found a mathematical model for such a machine with very complicated rules on a cartesian grid. Conway tried to simplify von Neumann's ideas and eventually succeeded. Coupling his previous success with Leech's problem in group theory with his interest in von Neuman's ideas concerning self-replicating machines resulted in the Game of Life.
It made its first public appearance in the October 1970 issue of Scientific American, in Martin Gardner's "Mathematical Games" column. From a theoretical point of view, it is interesting because it has the power of a universal Turing machine: that is, anything that can be computed algorithmically can be computed within Conway's Game of Life. It has often been claimed that since 1970 more computer time world-wide has been devoted to the Game of Life than any other single activity. Gardner wrote:
- "The game made Conway instantly famous, but it also opened up a whole new field of mathematical research, the field of cellular automata... Because of Life's analogies with the rise, fall and alterations of a society of living organisms, it belongs to a growing class of what are called "simulation games" - games that resemble real-life processes."
Ever since its publication, it has attracted much interest because of the surprising ways the patterns can evolve. Life is an example of emergence and self-organization. It is interesting for biologists, mathematicians, economists, philosophers and others to observe the way that complex patterns can emerge from the implementation of very simple rules.
Life has a number of recognised patterns which emerge from particular starting positions. Soon after publication several interesting patterns were discovered, including the ever-evolving F-pentomino (referred to as the "R-pentomino" in this context), the self-propelling "glider", and various "guns" which generate an endless stream of new patterns, all of which led to increased interest in the game. Its popularity was helped by the fact that it came into being just in time for a new generation of inexpensive minicomputers which were being released into the market, meaning that the game could be run for hours on these machines which were otherwise unused at night. In this respect it foreshadowed the later popularity of computer-generated fractals. For many aficionados Life was simply a programming challenge, a fun way to waste CPU cycles. For some, however, Life had more philosophical connotations. It developed a cult following through the 1970s and into the mid-1980s; current developments have gone so far as to create theoretic emulations of computer systems within the confines of a Life board.
Rules of Life
Conway chose his rules carefully, after a long period of experimentation, to meet three criteria:
- There should be no initial pattern for which there is a simple proof that the population can grow without limit.
- There should be initial patterns that apparently do grow without limit.
- There should be simple initial patterns that grow and change for a considerable period of time before coming to an end in the following possible ways:
- Fading away completely (from overcrowding or from becoming too sparse)
- Settling into a stable configuration that remains unchanged thereafter, or entering an oscillating phase in which they repeat an endless cycle of two or more periods.
In other words, the rules should be such as to make the behavior of the population both interesting and unpredictable.
The rules are simple and elegant:
- Any live cell with less than two neighbors dies of loneliness.
- Any live cell with more than three neighbors dies of crowding.
- Any dead cell with exactly three neighbors comes to life.
- Any live cell with two or three neighbors lives, unchanged, to the next generation.
It is important to understand that all births and deaths occur simultaneously. Together they constitute a single generation or, we could call it, a "tick" in the complete "life history" of the initial configuration.
Description
The "game" is actually a zero-player game, meaning that its evolution is determined by its initial state, needing no input from human players. It runs on a grid of squares ("cells") which stretches to infinity in all directions. Each cell has eight "neighbours", which are the cells adjacent to it, including diagonally. Each cell can be in one of two states: it is either "alive" or "dead". (The terms "on" and "off" are also used.) The state of the grid evolves in discrete time steps. The states of all of the cells at one time are taken into account to calculate the states of the cells one time step later. All of the cells are then updated simultaneously.
The transitions depend only on the number of live neighbours:
- A dead cell with exactly 3 live neighbours becomes alive (or is "born").
- A live cell with 2 or 3 live neighbours stays alive; otherwise it dies (from "loneliness" or "overcrowding").
The Game
The basic idea of the "game" is to start with a simple configuration of living cells (organisms) which are placed on a 2D grid by various methods. This constitutes the first generation. Conway's "genetic laws" for births, deaths and survivals (the four rules above) are then applied to the pattern and the next generation pattern is placed accordingly. Generation by generation the "player(s)" observe the various patterns that emerge.
Life goes on... and on...
From an initial pattern of living cells on the grid, you will find, as the generations tick by, the population constantly undergoing unusual, sometimes beautiful and always unexpected, change. In a few cases the society eventually dies out (all living cells vanishing), although this may not happen until after a great many generations. Most initial patterns either reach stable figures - Conway calls them "still lifes" - that cannot change or patterns that oscillate forever. Patterns with no initial symmetry tend to become symmetrical. Once this happens the symmetry cannot be lost, although it may increase in richness.
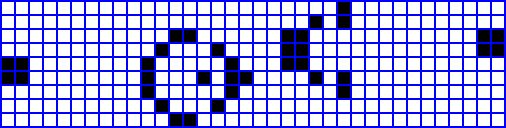
Conway originally conjectured that no pattern can grow without limit. Put another way, any configuration with a finite number of counters cannot grow beyond a finite upper limit to the number of counters on the field. This was probably the deepest and most difficult question posed by the game at the time. Conway offered a prize of $50 to the first person who could prove or disprove the conjecture before the end of 1970. One way to disprove it would be to discover patterns that keep adding counters to the field: A "gun" (a configuration that repeatedly shoots out moving objects such as the "glider") or a "puffer train" (a configuration that moves but leaves behind a trail of "smoke"). The prize was won in November of the same year by a team from M.I.T. The initial configuration (shown below) grows into such a gun, emitting the first glider on the 40th generation. The gun emits a new glider every 30th generation from then on.
Examples of patterns
GameOfLife.GIF
There are all sorts of different patterns that occur in the Game of Life, including static patterns ("still lifes"), repeating patterns ("oscillators" - a superset of still lifes), and patterns that translate themselves across the board ("spaceships"). The simplest examples of these three classes are shown below, with live cells shown in black, and dead cells shown in white.
 |
 |
 |
 |
Missing image Game_of_life_glider.png image:game_of_life_glider.png |
Missing image Game_of_life_lwss.png image:game_of_life_lwss.png |
| Block | Boat | Blinker | Toad | Glider | LWSS |
The "block" and "boat" are still lifes, the "blinker" and "toad" are oscillators, and the "glider" and "lightweight spaceship" ("LWSS") are spaceships which steadily march their way across the grid as time goes on.
Patterns called "Methuselahs" can evolve for long periods before repeating. "Diehard" is a pattern that eventually disappears after 130 generations, or steps. "Acorn" takes 5206 generations to generate 13 gliders then stabilises as many oscillators.
In the game's original appearance in "Mathematical Games", Conway offered a cash prize for any patterns that grew indefinitely. The first of these was found by Bill Gosper in November 1970. They include "guns", which are stationary and shoot out gliders or other spaceships; "puffers", which move along leaving behind a trail of debris; and "rakes", which move and emit spaceships. Gosper also later discovered a pattern with a quadratic growth rate, called a "breeder", which worked by leaving behind a trail of guns. Since then, various complicated constructions have been made, including glider logic gates, an adder, a prime number generator, and a unit cell which emulates the Game of Life at a much larger scale and slower pace.
The first glider gun found is still the smallest one known:
Simpler patterns were later found that also have infinite growth. All three of the following patterns have infinite growth. The first two create one blocklaying switch engine each, while the third creates two. The first has only 10 live cells (which has been proven to be minimal). The second fits in a 5 x 5 square. The third is only 1 cell high:
It is possible for gliders to interact with other objects in interesting ways. For example, if two gliders are shot at a block in just the right way, the block will move closer to the source of the gliders. If three gliders are shot in just the right way, the block will move further away. This "sliding block memory" can be used to simulate a counter. It is possible to construct logic gates AND, OR and NOT using gliders. It is possible to build a pattern which acts like a finite state machine connected to two counters. This has the same computational power as a universal Turing machine (see counter for the proof), so the Game of Life is as powerful as any computer with unlimited memory: it is Turing complete. Furthermore, a pattern can contain a collection of guns that combine to construct new objects, including copies of the original pattern. A "universal constructor" can be built which contains a Turing complete computer, and which can build many types of complex objects, including more copies of itself. (Descriptions of these constructions are given in Winning Ways by Conway, Elwyn Berlekamp and Richard Guy.)
Algorithms
The earliest results in the Game of Life were obtained without the use of computers. The simplest still-lifes and oscillators were discovered while tracking the fates of various small starting configurations using graph paper, blackboards, physical game boards and pieces, and the like. During this early research, Conway discovered that the R-pentomino failed to stabilize in a small number of generations.
These discoveries inspired computer programmers the world over to write programs to track the evolution of Life patterns. Most of the early algorithms were very similar. They represented Life patterns as two-dimensional arrays in computer memory. Typically two arrays are used, one to hold the current generation and one in which to calculate its successor. Often 0 and 1 represent dead and live cells, respectively. A double loop considers each element of the current array in turn, counting the live neighbors of each cell to decide whether the corresponding element of the successor array should be 0 or 1. At the end of this process, the contents of the successor array are moved to the current array, the successor array is cleared, and the current array is displayed.
A variety of minor enhancements to this basic scheme are possible, and there are many ways to save unnecessary computation. A cell that did not change at the last time step, and none of whose neighbors changed, is guaranteed not to change at the current time step as well, so a program that keeps track of which areas are active can save time by not updating the inactive zones.
In principle, the Life field is infinite, but computers have finite memory, and usually array sizes must be declared in advance. This leads to problems when the active area encroaches on the border of the array. Programmers have used several strategies to address these problems. The simplest strategy is simply to assume that every cell outside the array is dead. This is easy to program, but leads to inaccurate results when the active area crosses the boundary. A more sophisticated trick is to consider the left and right edges of the field to be stitched together, and the top and bottom edges also. The result is that active areas that move across a field edge reappear at the opposite edge. Inaccuracy can still result if the pattern grows too large, but at least there are no pathological edge effects. Techniques of dynamic storage allocation may also be used, creating ever-larger arrays to hold growing patterns. Alternatively, the programmer may abandon the notion of representing the Life field with a 2-dimensional array, and use a different data structure, like a vector of coordinate pairs representing live cells. This approach allows the pattern to move about the field unhindered, as long as the population does not exceed the size of the live-coordinate array. The drawback is that counting live neighbors becomes a search operation, slowing down simulation speed. With more sophisticated data structures this problem can also be largely solved.
For exploring very large patterns at very great time depths, sophisticated algorithms like Hashlife may be useful.
Variations on Life
Diamonds.png
Seeds.png
Conway.png
Since life's original inception, new rules have been developed. The standard Game of Life, in which a cell is "born" if it has exactly 3 neighbors, stays alive if it has 2 or 3 alive neighbors, and dies otherwise, is symbolized as "23/3". The first number, or list of numbers, is what is required for a cell to continue. The second set is the requirement for birth. Hence "16/6" means "a cell is born if there are 6 neighbours, and lives on if there are either 1 or 6 neighbours". HighLife is therefore 23/36, because having 6 neighbors, in addition to the original game's 23/3 rule, causes a birth. HighLife is most well known for its replicators. Additional variations on life exist, although the vast majority of these universes are either too chaotic or desolate.
- /3 (stable) almost everything is a spark
- 5678/35678 (chaotic) diamonds, catastrophes
- /2 (exploding) "Seeds" phoenix, minimal
- /234 (exploding) phoenix, lacey patterns
- 12345/3 (exploding) maze-like designs
- 125/36 (chaotic) Life-like 2x2 block rule
- 1357/1357 (exploding) everything is a replicator
- 1358/357 (chaotic) a balanced amoeba rule
- 23/3 (chaotic) "Conway's Life"
- 23/36 (chaotic) "HighLife" (has replicator)
- 235678/3678 (stable) ink blot, quick drying
- 235678/378 (exploding) coagulations in chaos
- 238/357 (chaotic) broken life
- 245/3 (chaotic) different patterns to Conway's Life
- 245/368 (stable) death plus puffers and ships
- 34/34 (exploding) "34 Life" was initially thought to be stable, but certain simple patterns did not terminate. Eventually, with modern computers, this proved to be the rule not the exception.
- 34678/3678 (exploding) "Day & Night"
- 4567/35678 (exploding) fast growth - interesting results when rules are changed to 456/35678
- 456/35678 (stable) decays surprisingly slowly when given a 4567/35678 input
- 45678/3 (exploding) slow coral growth
- 5/346 (stable) "Long life"
Source for this list of rules: Life32
Note that any automaton of the above form that contains the element /1 (e.g. 78/17, or 34/145) will always be explosive for any finite pattern - consider at minimum a single alive cell, and its eight neighbours in the Moore neighbourhood will enter the alive state in the next time step as they are all adjacent to the single cell. It is not possible to construct a finite pattern such that all dead cells have either zero (except the pattern where all cells are dead), or more than two living neighbours.
Additional variations have been designed by modifying other elements of the universe. The above variations can be thought of as 2D Square, because the world is two-dimensional and laid out in a square grid. 3D Square and 1D Square variations have been developed, as have 2D Hex variations where the grid is hexagonal or triangular instead of square.
Patterns
125/36
| Missing image 125-3_o1.gif Image:125-3_o1.gif | Missing image 125-36_o1.gif Image:125-36_o1.gif | Missing image 125-36_o2.gif Image:125-36_o2.gif |
245/3 (245/36)
| Missing image 24_3_3.gif Image:24 3_3.gif | Missing image 24_3_1.gif Image:24 3_1.gif | Missing image 24_3_2.gif Image:24 3_2.gif | Missing image O_24-3_4.gif Image:O 24-3_4.gif | Missing image 245-3_O1.gif Image:245-3_O1.gif | Missing image 245-3_O2.gif Image:245-3_O2.gif | Missing image 245-3_qualle.gif Jelly fish |
See also
- Garden of Eden pattern
- hashlife
- Immigration
- Life-like cellular automaton
- Spaceship
- QuadLife
- Puffer train
Bibliography
Some text, such as the rules were taken from a Life version coded in Microsoft Visual Basic. The author of the software is unknown, but if he sees this and recognizes, please feel free to edit this.
External links
- Life Lexicon (http://www.argentum.freeserve.co.uk/lex.htm)
- Conway's Game of Life applet software home page (http://www.ibiblio.org/lifepatterns/)
- Article suggesting that Conway's Game of Life is "inordinately analogous to the workings of the female reproductive system." (http://www.adequacy.org/public/stories/2002.5.16.143527.295.html)
- "Eric Weisstein's Treasure Trove of the Life C.A. (http://www.ericweisstein.com/encyclopedias/life/)" - a site by Dr. Eric Weisstein containing many descriptions and animations of Life patterns
- Game of Life applet with source code (http://www.bitstorm.org/gameoflife/)
- Wonders of Math - The Game of Life (http://www.math.com/students/wonders/life/life.html)
- Grant Robinson's Cellular Automata (http://grant.robinson.name/projects/cellularAutomata/) Game of Life done in ActionScript / Flash
- Color Game of Life Visual Exhibition (http://www.collidoscope.com/cgolve/) Color pattern collection and a fast Java applet
- Live color demonstrations of Life-like rule variations (http://www.collidoscope.com/modernca/lifelikerules.html) Java powered
- The turing machine, implemented in game of life. (http://rendell.server.org.uk/gol/tm.htm)
- 3D Game of Life visualizer written in Smalltalk (http://www.softcentral.com/informationspace/)
- A Brief Illustrated Glossary of Terms in Conway's Game of Life (http://www.radicaleye.com/lifepage/picgloss/picgloss.html)
- Cliff Reiter's implementation (http://ww2.lafayette.edu/~reiterc/j/vector/vlife_index.html) in the J Programming Language
- 3D Game of Life in Java (http://ibiblio.org/e-notes/Life/Game.htm)
- Mushroom Life in Flash (http://a.parsons.edu/~joseph/k2/gameoflife)
- GtkLife (http://ironphoenix.org/tril/gtklife/) An open-source Game of Life program for Unix-like operating systems
- http://www.argentum.freeserve.co.uk/lex.htm -- An interesting lexicon concerning the terminology of "Life".
- http://www.ibiblio.org/lifepatterns/ -- A Java Life Simulation applet and a large amount of patterns to try.de:Game of Life
es:Juego de la vida fr:Le jeu de la vie ia:Joco del Vita de Conway it:Gioco life di Conway ja:ライフゲーム ko:라이프 게임 nl:Game of Life pl:Gra w życie ru:Жизнь (игра) sv:Game of Life zh:生命游戏