Archimedean solid
|
|
In geometry an Archimedean solid or semi-regular solid is a semi-regular convex polyhedron composed of two or more types of regular polygon meeting in identical vertices. They are distinct from the Platonic solids, which are composed of only one type of polygon meeting in identical vertices, and from the Johnson solids, whose regular polygonal faces do not meet in identical vertices.
Origin of name
The Archimedean solids take their name from Archimedes, who discussed them in a now-lost work. During the Renaissance, artists and mathematicians valued pure forms and rediscovered all of these forms. This search was completed around 1619 by Johannes Kepler, who defined prisms, antiprisms, and the non-convex solids known as Kepler-Poinsot solids.
Classification
There are 13 Archimedean solids (15 if the mirror images of two enantiomorphs, see below, are counted separately). Here the vertex configuration refers to the type of regular polygons that meet at any given vertex. For example, a vertex configuration of (4,6,8) means that a square, hexagon, and octagon meet at a vertex (with the order taken to be clockwise around the vertex).
| Name and picture | Faces | Edges | Vertices | Vertex configuration | Symmetry group | |
|---|---|---|---|---|---|---|
cuboctahedron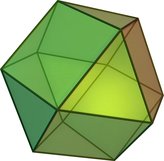 (Video) | 14 | 8 triangles 6 squares | 24 | 12 | 3,4,3,4 | Oh |
| icosidodecahedron Missing image Icosidodecahedron.jpg Icosidodecahedron (Video) | 32 | 20 triangles 12 pentagons | 60 | 30 | 3,5,3,5 | Ih |
| truncated tetrahedron Missing image Truncatedtetrahedron.jpg Truncated tetrahedron (Video) | 8 | 4 triangles 4 hexagons | 18 | 12 | 3,6,6 | Td |
| truncated cube or truncated hexahedron Missing image Truncatedhexahedron.jpg Truncated hexahedron (Video) | 14 | 8 triangles 6 octagons | 36 | 24 | 3,8,8 | Oh |
truncated octahedron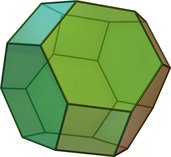 (Video) | 14 | 6 squares 8 hexagons | 36 | 24 | 4,6,6 | Oh |
| truncated dodecahedron Missing image Truncateddodecahedron.jpg Truncated dodecahedron (Video) | 32 | 20 triangles 12 decagons | 90 | 60 | 3,10,10 | Ih |
| truncated icosahedron or commonly football (soccer ball) Missing image Truncatedicosahedron.jpg Truncated icosahedron (Video) | 32 | 12 pentagons 20 hexagons | 90 | 60 | 5,6,6 | Ih |
| rhombicuboctahedron or small rhombicuboctahedron  (Video) | 26 | 8 triangles 18 squares | 48 | 24 | 3,4,4,4 | Oh |
| truncated cuboctahedron or great rhombicuboctahedron 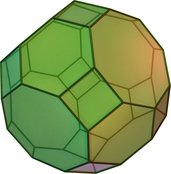 (Video) | 26 | 12 squares 8 hexagons 6 octagons | 72 | 48 | 4,6,8 | Oh |
| rhombicosidodecahedron or small rhombicosidodecahedron  (Video) | 62 | 20 triangles 30 squares 12 pentagons | 120 | 60 | 3,4,5,4 | Ih |
| truncated icosidodecahedron or great rhombicosidodecahedron Missing image Truncatedicosidodecahedron.jpg Truncated icosidodecahedron (Video) | 62 | 30 squares 20 hexagons 12 decagons | 180 | 120 | 4,6,10 | Ih |
| snub cube or snub cuboctahedron (2 chiral forms)  (Video)  (Video) | 38 | 32 triangles 6 squares | 60 | 24 | 3,3,3,3,4 | O |
| snub dodecahedron or snub icosidodecahedron (2 chiral forms)  (Video) Missing image Snubdodecahedroncw.jpg Snub dodecahedron (Cw) (Video) | 92 | 80 triangles 12 pentagons | 150 | 60 | 3,3,3,3,5 | I |
The first two solids (cuboctahedron and icosidodecahedron) are edge-uniform and are called quasi-regular.
The last two (snub cube and snub dodecahedron) are known as chiral, as they come in a left-handed (Latin: levomorph or laevomorph) form and right-handed (Latin: dextromorph) form. When something comes in multiple forms which are each other's three-dimensional mirror image, these forms may be called enantiomorphs. (This nomenclature is also used for the forms of chemical compounds).
The duals of the Archimedean solids are called the Catalan solids. Together with the bipyramids and trapezohedra, these are the face-uniform solids with regular vertices.
External links
- Paper models of Archimedean solids (http://www.software3d.com/Archimedean.html)
- The Uniform Polyhedra (http://www.mathconsult.ch/showroom/unipoly/)
- Virtual Reality Polyhedra (http://www.georgehart.com/virtual-polyhedra/vp.html) The Encyclopedia of Polyhedra
- Penultimate Modular Origami (http://www.cs.utk.edu/~plank/plank/origami/penultimate/intro.html)
- Interactive 3D polyhedra (http://ibiblio.org/e-notes/3Dapp/Convex.htm) in Javade:Archimedischer Körper
it:Solido archimedeo nl:Halfregelmatig veelvlak pl:Wielościan półforemny ru:Полуправильный многогранник zh:半正多面體
