User:Hhanke
|
|
Hi, I'm Hynek Hanke and I come from Prague, Czech Republic.
| Contents |
About me
I'm a student of physics on the Faculty of mathematics and physics on the Charles university.
My hobbies
In my free time, I code Free Software programs to help the blind and visually impaired people (http://www.freebsoft.org). I also like to think about the nature and her beauty, do some experiments with her (electricity, laser, mechanics), watch her night sky and hike through her. I don't believe hiking in forest is fundamentaly different from doing atomic physics and some people laugh to me because of that. And I don't mind because "What do you care what other people thing?" :)
I enjoy solving math problems and playing chess.
Free Software, GNU/Linux, collaborative projects like Wikipedia
My favourite problems
- Continue the sequence: 0 1 2 720! ? (! means factorial)
- Continue the sequence: k d m k d m v h p l b s ? (only for Czechs or for cryptography maniacs)
- Why is the sky blue? (oxygen is not blue :)
- If you dig a hole through the Earth from the south pole to the north pole, what will happen if you jump into it? Will you ever return to your starting place? In what time? (assume homogeneous perfectly sphreetical Earth etc.)
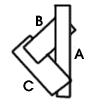
- How does the side-view look?
The front-view (above the axis) and the top-view (bellow the axis) of an object. The object is real and can be fabricated from e.g. wood, there are no infinitely thin sides. All painted edges are visible. How does the side-view look? :)
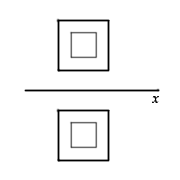
- Where is the missing square? In the pub???
Problem-geometry-2.png
- There are two mathematicians: Alice and Bob. Also, there are two natural numbers: x and y. The problems is that alice knows only how much is x+y and Bob knows only the value of x*y. Then the following strange conversation takes place:
- Alice: I don't know the numbers.
- Bob: I don't know the numbers either.
- Alice: Now I know the numbers.
- Bob: I also know the numbers.
Then, out of all the happiness of finding the solution in such an elegant way, Alice kisses Bob, and Bob realizes kissing is commutative. But for the reader the question is still hanging out there in the air: What is the value of x and y?
- There are 12 balls, looking exactly the same, but one of them is either lighter or heavier. You are given balances and in 3 tries, you should determine which of the ball is the defect one and if it is lighter of heavier.
How do you do that? Can you generalize: How many balls can one possibly handle in n tries?
- My friend once conjunctured, that if you write out a sequence of 0's and 1's in such a way, that you always start with a 1 and then in the next steps, you expand the sequence by the following rules:
- for each 1 you have written down in the previous step, you write down two figures
- for each 0 you have written down in the previous step, you write down only one figure
- the packets of one or two figures must alternate between 1 and 0
then in this infinitely long sequence of 0's and 1's, you can never find a subsequence that would repeat itself three times consecutively. An example of how you construct the sequence (the vertical lines are there only to suggest the packets that come from each step and are not a part of the sequence):
- 1
- 1|00
- 1|00|10
- 1|00|10|110
- 1|00|10|110|11001
- 1|00|10|110|11001|11001011
- ...
The conjuncture says, that you will never find in this sequence for example a subsequence like:
- 111
- 101010
- 101101101
- 011011011
- ...
Can you prove or disprove that? [I myself don't know the proof, but I couldn't even find a counterexample. I don't know if a proof or counterexample is known.]
If you also have a favourite problem, please let me know on my talk page (we could even once establish an article about such problems). If you are realy desperate and want to ask me about the solution of some of these questions, please drop me an email on hanke in volny point cz.
Other projects I like
- Hospitality Club
- http://hebb.mit.edu/FreeMusic MIT and Pandora archives of classical Free music.
Un-ordinary people
- Eva Frantova, my roller skating teacher, one of the fortunes and misfortunes of my life.
- Richard Feynman, my teacher of physics (througth his books)
- Paul Erdos, my teacher of how not to stick to stupidities (through the stories about him)
- Salvador Rodriguez Martin, my teacher of mathematics
- Richard Stallman, Donald Knuth, my teachers of programming ethics (through how they live and what they do)
Me and Wikipedia
I also like to browse, read and edit Wikipedia
The articles I have started
Jaroslav Foglar Spanish literature Mester de Juglaría Mester de Clerecía Gonzalo de Berceo Jorge Manrique Matrix representation of conic sections Painter's algorithm
The articles I have contributed to
One World Talk:Color blindness Miguel de Unamuno
The images and photos I have made for Wikipedia
Slide_rule_cursor.jpg
