Unimodular matrix
|
|
In mathematics, a unimodular matrix is a square matrix with determinant +1 or -1.
A totally unimodular matrix is an integer matrix for which every square non-singular submatrix is also unimodular.
An integer program whose constraint matrix is totally unimodular and whose right hand side is integral, can be solved efficiently since its LP relaxation gives rise to integer solutions.
Example
- <math>A=\begin{bmatrix}
-1 & -1 & 0 & 0 & 0 & +1\\
+1 & 0 & -1 & -1 & 0 & 0\\
0 & +1 & +1 & 0 & -1 & 0\\
0 & 0 & 0 & +1 & +1 & -1\\
\end{bmatrix}<math>
is an example of a totally unimodular matrix. It arises as the constraint matrix of the linear programming formulation (without the capacity constraint) of the maximum flow problem on the following network:
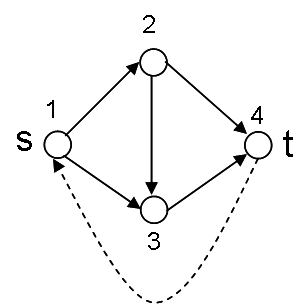
This matrix <math>A<math> had the following properties:
- all its entries are either 0,-1 or +1;
- any column has at most two nonzero entries;
- the columns with two nonzero entries have entries with opposite sign.
Those properties are sufficient for a matrix to be totally unimodular (but they are not necessary). Any network flow problem will yield a constraint matrix with the above structure (so that's why any network flow problem with bounded integer capacities has an integer optimal value).
References
Christos H. Papadimitriou and Kenneth Steiglitz, Combinatorial Optimization: Algorithms and Complexity, Section 13.2, Dover Publications, Mineola NY, 1998. ISBN 0-486-40258-4
External reference
See a Mathematical Programming Glossary (http://carbon.cudenver.edu/~hgreenbe/glossary/second.php?page=U.html) by Harvey J. Greenberg.
