Thales' theorem
|
|
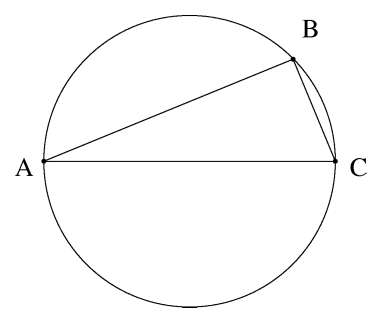
In geometry, Thales' theorem (named after Thales of Miletus) states that if A, B and C are points on a circle where the line AC is a diameter of the circle, then the angle ABC is a right angle.
| Contents |
Proof
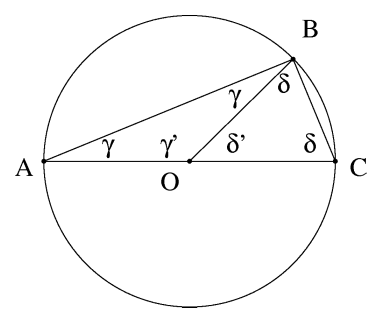
We use the following facts: the sum of the angles in a triangle is equal to two right angles and that the base angles of an isosceles triangle are equal.
Let O be the center of the circle. Since OA = OB = OC, OAB and OBC are isosceles triangles, and by the equality of the base angles of an isosceles triangle, OBC = OCB and BAO = ABO. Let γ = BAO and δ = OBC.
Since the sum of the angles of a triangle is equal to two right angles, we have
- 2γ + γ ′ = 180°
and
- 2δ + δ ′ = 180°
We also know that
- γ ′ + δ ′ = 180°
Adding the first two equations and subtracting the third, we obtain
- 2γ + γ ′ + 2δ + δ ′ − (γ ′ + δ ′) = 180°
which, after cancelling γ ′ and δ ′, implies that
- γ + δ = 90°
Converse
The converse of Thales' theorem is also valid, which states that a right triangle's hypotenuse is a diameter of its circumcircle.
The theorem and its converse can be expressed as follows:
- The center of the circumcircle of a triangle lies on one of the triangle's sides if and only if the triangle is a right triangle.
Proof of the converse
The proof utilises the fact that directional vectors of two lines form right angles if and only if the dot product is zero. Let there be a right angle ABC and circle M with AC as a diameter. Let M's center lie on the origin, for easier calculation. Then the dot product of AB and BC is:
(A - B) · (B - C) = (A - B) · (B + A) = |A|2 - |B|2 = 0
Hence:
|A| = |B|
A and B are also equidistant from the circle's center, hence M is the triangle's circumcenter.
Generalization
Thales' theorem is a special case of the following theorem: given three points A, B and C on a circle with center O, the angle AOC is twice as large as the angle ABC.
History
Thales was not the first to discover this theorem since the Egyptians and Babylonians must have known of this empirically. However they did not prove the theorem, and the theorem is named after Thales because he was said to have been the first to prove the theorem, using his own results that the base angles of an isosceles triangle are equal, and that the sum of angles in a triangle is equal to two right angles.
See also
de:Satz des Thales es:Teorema de Tales fr:Théorème de Thalès (cercle) sl:Talesov izrek sr:Талесова теорема uk:Теорема Фалеса zh:泰勒斯定理