Tangent
|
|
In mathematics, the word "tangent" has two distinct, but etymologically related meanings: one in geometry, and one in trigonometry.
| Contents |
Geometry
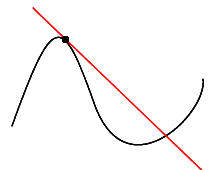
In plane geometry, a straight line is tangent to a curve, at some point, if both line and curve pass through the point with the same direction; such a line is the best straight-line approximation to the curve at that point. The curve, at point P, has the same slope as a tangent passing through P. The slope of a tangent line can be approximated by a secant line. It is a mistake to think of tangents as lines which intersect a curve at only one single point. There are tangents which intersect curves at several points (as in the following example), and there are non-tangential lines which intersect curves at only one single point. (Note that in the important case of a circle, however, the tangent line will intersect the curve at only one point.)
In the following diagram, a red line intersects the black curve at two points. It is tangent to the curve at one point.
In higher-dimensional geometry, one can define the tangent plane for a surface in an analogous way to the tangent line for a curve. In general, one can have an (n - 1)-dimensional tangent hyperplane to an (n - 1)-dimensional manifold.
Quote
"And I dare say that this is not only the most useful and general [concept] in geometry, that I know, but even that I ever desire to know." Descartes (1637)
Calculus
A "formal" definition of the tangent requires calculus. Specifically, suppose a curve is the graph of some function, y = f(x), and we are interested in the point (x0, y0) where y0 = f(x0). The curve has a non-vertical tangent at the point (x0, y0) if and only if the function is differentiable at x0. In this case, the slope of the tangent is given by f '(x0). The curve has a vertical tangent at (x0, y0) if and only if the slope approaches plus or minus infinity as one approaches the point from either side.
Above, it was noted that a secant can be used to approximate a tangent; it could be said that the slope of a secant approaches the slope (or direction) of the tangent, as the secants' points of intersection approach each other. Should one also understand the notion of a limit; one might understand how that concept is applicable to those discussed here, via calculus. In essence, calculus was developed (in part) as a means to find the slopes of tangents; this challenge, being known as the tangent line problem, is solvable via Newton's difference quotient.
Should one know the slope of a tangent, to some function; then, one can determine an equation for the tangent. For example, an understanding of the power rule will help one determine that the slope of x3, at x = 2, is 12. Using the point-slope equation, one can write an equation for this tangent: y - 8 = 12(x - 2) = 12x - 24; or: y = 12x - 16
Trigonometry
In trigonometry, the tangent is a function (see trigonometric function) defined as:
- <math>\,\tan x = \frac{\,\sin x}{\,\cos x}<math>
The function is so-named because it can be defined as the length of a certain segment of a tangent (in the geometric sense) to the unit circle. It is easiest to define it in the context of a two-dimensional Cartesian coordinate system. If one constructs the unit circle centred at the origin, the tangent line to the unit circle at the point P = (1, 0), and the ray emanating from the origin at an angle θ to the x-axis, then the ray will intersect the tangent line at at most a single point Q. The tangent (in the trigonometric sense) of θ is the length of the portion of the tangent line between P and Q. If the ray does not intersect the tangent line, then the tangent (function) of θ is undefined.
Derivative
The derivative of the tangent is:
- <math>\,\frac{\mathrm{d} (\tan x)}{\mathrm{d} x} = \frac{1}{\cos^2 x}=\sec^2 x.<math>
See also
External link
- MathWorld: Tangent (http://mathworld.wolfram.com/Tangent.html)da:Tangent
de:Tangente es:Tangente fr:Tangente pl:Styczna sv:Tangent zh:切线