Talk:Twin paradox
|
|
I reverted to an earlier version (including the better moving clock example of muons). I removed this:
It turns out that twin positions are not symmetrical. One is twin never accelerates, while the other twin moves away, changes direction and returns back. Although some have incorrectly stated otherwise, this problem is perfectly solvable using special relativity. Using special relativity one can calculate the elapsed time in the reference frame of each twin and the twin who moves away and comes back will have the shorter elapsed time.
Consider a spaceship that travels to a star four light years away in five years and returns five years later. In the reference frame of earth, the spaceship leaves at (x=0, t=0), moves to the star at (x=4, t=5), and returns to earth at (x=0, y=10). The time elapsed for the person on earth is 10 years.
Now let us look at things from the reference frame of the spaceship. The key equation in special relativity is that the spacetime interval (s^2 = x^2 - t^2) is the same in all reference frames. Consider the spaceship moving to the star. In the reference frame of the ship, its position (x') is fixed. Thereform the time elapse t' must obey the equation - t'^2 = x^2 - t^2, which means that in the reference frame of the ship, three years have elapsed between leaving earth and reaching the star. Using a similar argument, one can see that the time elapsed in moving from the star to the earth is also three years. Hence in the reference frame of the ship, six years have elapsed.
This paragraph does not resolve the paradox at all: From the viewpoint of the ship, the brother on Earth is moving away, then coming back. So the twin on the ship could perform the exact same analysis as given above, but with roles of the twins reversed, and would conclude that the "trip" by the brother on earth will be seen from the ship as being longer than it is experienced on Earth itself. The crucial difference between the brothers is that one sits in an inertial frame, the other doesn't. --AxelBoldt
This just in from someone who created a duplicate article:
The Twin's Paradox is a classic problem concerning apparant violations of Special Relativity, which posits that no privileged frames of reference exist in the universe with regards to motion.
The basic idea is this: one of a pair of twins blasts off on a spaceship and accelerates to near light-speed, travels around some nearby stars, and then returns to find his sibling greatly aged due to time dilation. The question is, if there are no privileged frames of reference, why does only one of the twins age? Couldn't the twin who was travelling say that he was at rest, and it was his sibling that was in motion?
The correct Lorentz transformations are provided by including General Relativity, since accelerating objects reside in warped spacetime, and must take that into account to fully describe their frames of reference. The paradox results from only taking differences in the twins' positions into account, and not their respective local spacetime curvatures.
See also: acceleration
I don't understand why the "accelerating" twin couldn't be interpreted as being stionary while the "staionary" twin is interpreted as accelerating. Maybe I don't understand this stuff, but it always seemed to me that the center of the universe (the origin of the big bang) could be used as a central point of reference by which to measure the relative movement of all things inside it...?
SR has such a revered place in physics that any attempt to suggest that it might be "silly" or "wrong" will only meet with scorn from the establishment who then try anything to save it. The twins paradox is an example of this. Two dictionary definitions of a paradox are : (i) a seemingly absurd statement that is actually based on truth; (ii) a statement contrary to accepted opinion.
Thus (i)the establishment are telling us that the reality is true (the spaceship twin ages faster) even though SR predicts that both clocks will slow down equally and (ii) denying the truth of SR is wrong because it is contrary to accepted opinion i.e.theirs.
The earth and the spaceship are two inertial frames moving with relative constant velocity. While they continue to move like this, SR predicts that the clock on the spaceship will run slow compared to a clock on earth. SR also predicts that the clock on earth will run slow compared to the clock on the spaceship. The two predictions are mutually inconsistent and thus the apparent paradox is not really a paradox at all. The notion that the spaceship twin ages faster is just wrong, and that is all there is to it!
The explanation involving acceleration is just a red herring. The conclusion (differential aging) is predicted by an equation that does not depend on acceleration and so acceleration is irrelevant.
- One source of confusion is the fact that time and space must not be viewed separately. Best to forget about time dilation and length contraction formulas and stick to the Lorentz transformation of coordinate points in spacetime.
- Think of two identical light houses each one measurig the height of the other by looking horizontally for each others light.Now put them (on a moon or small planet) at a great distance from each other, so that they effectively point in different directions. Each of them will have to look down from the horizontal to see the others light an declare the other one to be the shorter.
I find the latest modification confusing. The separation of the three frames is indeed useful. But the analogy with the plane doesn't explain much, and the statement that the ordering of events depends on the reference frame might be easily misinterpreted (if there is a possible causal connection between two events, their order is fixed in all frames). I'm going to restore some of the previous text.
Bartosz 06:44, 13 Mar 2004 (UTC)
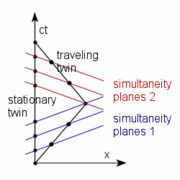
I added a standard spacetime diagram showing what happens. The whole article now seems full of repetitions. It should probably be rewritten by somebody with good editing skills.
Bartosz 08:38, 13 Mar 2004 (UTC)
| Contents |
From the POV of general relativity?
(William M. Connolley 21:53, 11 Jul 2004 (UTC)) I'm fairly happy with the page as it stands, and (probably) its contention that the paradox *can* be explained within SR. But I wonder what happens if you *do* explain the paradox within GR. The point is that then you can no longer say that the travelling twin switches frames. The laws are then the same for *all* observers, including one who accelerates. Doesn't this then end up linking time dilation from relative velocity to time dilation in gravity?
- I'm not clear what you mean by explaining the paradox with GR. You can construct a thought experiment in which twin A spends a long time out in flat spacetime while twin B goes deep into a gravity well, and then they rejoin and compare watches, but there's no 'paradox' since there's no way to flip it around so it seems that A's watch should be running slower than B's.
- (William M. Connolley 13:05, 12 Jul 2004 (UTC)) No, I don't mean that. I mean the same scenario as at present, but explained within GR. The current article explains the discrepancy - that both sides should be able to see the others clocks run slow - by the flip of frames at turnaround, and says that this is beacuse in SR you have to be in an inertial frame. Fair enough. But in GR you don't: the laws-of-physics are the same for *all observers*, accelerated or otherwise: so the "travelling" twin doesn't have to switch frames at turnaround.
- Something like this:
- The Twin Paradox: The "General Relativity" Explanation (http://math.ucr.edu/home/baez/physics/Relativity/SR/TwinParadox/twin_gr.html)?
- --wwoods 19:28, 12 Jul 2004 (UTC)
- (William M. Connolley 20:49, 12 Jul 2004 (UTC)) Yes, thats nice. Thanks. I shall ponder it.
- I'm not happy with the phrase, "the resting twin ages very fast". The stay-at-home twin isn't, of course, aging fast. It's just that the travelling twin calculates the time back home before and after his U-turn, and gets very different results.
- --wwoods 22:56, 11 Jul 2004 (UTC)
(Onerock 19:40, 28 Jul 2004 (UTC)) The so-called Twins Paradox, related at the end of a lecture on special relativity, was Einstein’s idea of a joke and a test to see who was paying attention. He hadn’t even begun working on his general theory, yet. The one or two members of the audience who laughed understood that you can’t apply special relativity to a round-trip problem. I mean, how can you go from A to B and back to A without accelerating? Ha, haa, haaaaaa! That ol’ Alf sure knows how to tell ‘em, don’t he! He, heee! What a comedian! I gotta try that one at the improv’. It can’t go over any worse there than it did at all the major universities of the world. Even today, many serious scientists are trying to “explain” the “paradox” when they should be having a good laugh. P.S.: I'm new to Wiki, so please excuse my syntactic flubs.
It seems to me this paradox is 'solved' by the fact that the space ship twin went through acceleration at the start and at the midpoint of his travel. While this would seem to be a neat solution, there is something with troubles me greatly, yet I find it unlikely that it has not been explained in the history of SR. For illustration sake, I will use human examples in my question:
So the twin takes off from earth in his space ship and soon reaches an inertial frame with constant-velocity. He travels for 20 of his years, and turns the ship around to head home. After turning around and reaching a constant velocity again with a path toward Earth, he and his wife (who he brought along) have a child in the spaceship. This child grows up in the spaceship and will arrive at Earth in 20 years of his time. All his life he could look through his telescope at Earth and see how rapidly it was coming towards him, since he observes his spaceship to be quite stationary. When this 20 year old arrives at Earth, what would he discover?
Or even more plainly, would this child see people on Earth moving at ultra-rapid time or would he see them moving ultra-slow, assuming he had a telescope good enough to see individual people on the planet?
This eliminates all the nonsence about the importance of acceleration. Obviously the actions of the child's father in the past and his take off from Earth in the past shouldn't affect the child's frame of reference. All he knows is that he's in a stationary ship and he sees Earth coming at him through the window, right?
I point out that "turning around" is also an irrelevant discussion. Since without the ship turning around, the two brothers can send each other information (at the speed of light) as to how old they are. Therefore they can determine who is the one actually aging faster without turning around. If acceleration is the problem, the twin on earth can have a child at the exact same time his brother on the ship does, and the two sons, who never experienced acceleration can send each other messages comparing ages.
I would be extremely grateful to anybody who can answer this question for me. Wodan 18:00, Aug 26, 2004 (UTC)
- The point is that the twins disagree on what is "the exact same time".
- Maybe the diagrams on this page will help you understand:
- Bvr 19:18, 2 Sep 2004 (UTC)
Then let me simplify the matter greatly. Two spaceships are in deep deep space. So deep that light from the rest of the universe has not even reach them yet. They are as far as all they can tell, with no other references. They look out the window of the spaceships and see that they are heading toward each other at great speeds. So to both it looks like he is stationary and the other one is moving, or vice versa, or some mix of speeds. How does relativity explain which one will be actually experience time dilation???
Wodan 01:22, Sep 3, 2004 (UTC)
- They both would. That is, they'd both see the other as being time-dilated. Well, they'd calculate the other as having been time-dilated, after they adjust their observations for relativistic Doppler effect. That's the essence of relativity—no (inertial) frame of reference is more valid than another. It's only when you bring them back together that you can compare their different experiences, and determine that while one has traveled farther in space, the other has traveled farther in time, so that from start to finish they've both travelled the same interval in spacetime.
- Try http://math.ucr.edu/home/baez/physics/Relativity/SR/TwinParadox/twin_paradox.html
- —wwoods 07:30, 3 Sep 2004 (UTC)
- * Then why does one move through time and one move through space? How does timespace decide which is moving through space and which is not, since it's impossible to observe either, and really, is rather meaningless since there is no reference whatsoever...?
- * Additionally, since there are no absolutes, me spinning around at night and watching all the stars in the universe is the same as the universe spinning around me, and no more or less valid. Then how is it that the universe just spun around me, since that would imply matter moving at much greater than the speed of light?
Wodan 19:52, Sep 3, 2004 (UTC)
- This is basically reiterating Wodan's scenario, but I'll give my example anyways. Two spaceships are attached with a (very large) elastic in "deep deep" space. Each is moving with a constant velocity according to the frame of reference at the centre of the elastic. When the elastic becomes taut and causes decceleration, the two spaceships are pulled to the same point in spacetime. Which one has aged more? Each observer observes themselves to be stationary and the other to be the one doing the deccelerating.
- PengRate 02:05, 2005 Jun 23 (UTC)
- Neither. Since the acceleration is being applied equally to both spaceships, the situation remains symmetric, and both spaceships have aged equally, both having aged less than the center of the elastic. --Carnildo 06:01, 23 Jun 2005 (UTC)
The first question is somewhat similar to asking, How does space decide whether I'm moving in the X or Y direction? It doesn't! You pick a coordinate system that's convenient for you. Having said that, the space-time coordinate system cannot be picked arbitrarily--you cannot exchange the time axis with any of the space axes. All you can do is to, figuratively, tilt the time axis by less than 45 degrees.
In the diagram in the article, you can make a transformation in which the first leg of the rocket's trajectory coincides with the time axis. In such a system of coordinates, the earthbound twin will be moving in space (leftward), and the traveler will be stationary. If fact that coordinate system is the inertial frame of the traveling twin during the first leg of the journey. Note that after the U-turn, in that coordinate system, he will start moving fast toward the "receding" earthbound twin and will eventually catch up with him. Equivalently, you can transform the coordinate system such that the second leg of the journey will coincide with the time direction. In that frame, the eartbound twin will be steadily moving towards the traveling twin.
The second question is a tough one. Einstein tried to address it in his general relativity, but failed. He wasn't able to derive the Mach's principle from his equations. So the question is still open.
Bartosz 18:31, 15 Oct 2004 (UTC)
Would someone please check the following example calculation?
A spaceship starts from space station Alpha flying to space station Beta at a fixed distance of 4 ligthyears. Then it flies back again. Both times it travels with a speed of <math>\frac45 c_0<math>. There are three events in spacetime, start at Alpha, arrival and simultanious departure at Beta, and rearival at Alpha. In the coordinate system of Alpha these have the representations <math>\left(\begin{matrix}0 \\ 0 \end{matrix}\right),<math> <math>\left(\begin{matrix}5 \\ 4 \end{matrix}\right)<math> and <math>\left(\begin{matrix}10 \\ 0 \end{matrix}\right).<math>
Now to obtain the representation of this events in the coordinate system of the spaceship by transforming the above coordinates with the appropriate Lorentz matrix. Measuring the distance in lightyears we have <math>c_0 = 1<math> which simpifies the matrix. For the flight from Alpha to Beta we have <math>v=-\frac45<math>, for the fligth back we have <math>v=\frac45<math>. This change of frames creates the asymmetry.
So <math>L_{\Alpha\to\Beta} = \gamma\left(\begin{matrix}1 & -\frac45 \\ -\frac45 & 1\end{matrix}\right)<math> wheras <math>L_{\Beta\to\Alpha} = \gamma\left(\begin{matrix}1 & \frac45 \\ \frac45 & 1\end{matrix}\right)<math> whith <math>\gamma = \frac53<math> both times.
<math>\left(\begin{matrix}0 \\ 0 \end{matrix}\right)<math> clearly transforms to itself. <math>L_{\Alpha\to\Beta}\left(\begin{matrix}5 \\ 4 \end{matrix}\right) = \left(\begin{matrix} 3 \\ 0 \end{matrix}\right)<math> and for the fliht back we have to compute the difference <math>L_{\Beta\to\Alpha}\left(\left(\begin{matrix}10 \\ 0 \end{matrix}\right) - \left(\begin{matrix}5 \\ 4 \end{matrix}\right)\right) = \left(\begin{matrix} 3 \\ 0 \end{matrix}\right).<math>
This results in a total of <math>\left(\begin{matrix}3 \\ 0 \end{matrix}\right) + \left(\begin{matrix} 3 \\ 0 \end{matrix}\right) = \left(\begin{matrix} 6 \\ 0 \end{matrix}\right),<math> so the frame-switching twin stays younger by 10 - 6 = 4 years.
The space component of the transformed coordinates always being zero is an additional check on the computation.
This calculation looks correct. One might mention that <math>\gamma = \frac{1}{\sqrt{1 - v^2 / c^2}}<math>, which in the example above becomes <math>\frac{1}{\sqrt{1 - 16/25}} = 5/3<math>.
Bartosz 22:25, 19 Oct 2004 (UTC)
- should the example calculation be moved to the article then? Some corrections on language should perhaps better be done by a native speaker 217.94.149.179 19:15, 20 Oct 2004 (UTC)
I think it's a good calculation for people who understand the math behind special relativity. For everybody else it's just black magic. One would have to explain the terms, notation, and most importantly the interpretation of the results--it's not really as simple as it looks. There are a lot of hidden assumptions made in this calculation, in particular about the connection between the vector being transformed and the subjective time of the observer (proper time). Physics is math + interpretation. Here we see naked math.
Bartosz 22:17, 21 Oct 2004 (UTC)
- I agree with what you say. On the other hand --- for most people the twin paradox will be black magic anyway.
- I am new to wiki and I don't want to argue about this special calculation but other articles do have computations and proofs. So where would be an apropriate place for "advanced" examples, calculations and proofs that are not of interrest for the majority of readers? 217.230.29.21 19:25, 24 Oct 2004 (UTC)
I didn't say it couldn't be published. It just needs quite a bit of additional work in order to be useful.
Bartosz 21:34, 24 Oct 2004 (UTC)
- I think now that wikibooks:Wikiversity:Special Relativity would finally be the best place for stuff like that. 217.230.21.104 11:13, 30 Oct 2004 (UTC)
Need for general relativity?
- It is sometimes claimed that the twin paradox cannot be resolved without the use of general relativity. Indeed, one of the twins must undergo acceleration during the U-turn, and only general relativity can properly describe accellerating observers. Strictly speaking this is true. Special relativity, however, is an excellent approximation to general relativity, except for very strong gravitational fields and large accellerations. If we can make the inertial legs of the trip long enough and the accelleration at the U-turn small enough, the effects of general relativity in the above analysis would amount to very small corrections.
- I don't get this. Why can't accelerating objects be described with special relativity?[1] (http://math.ucr.edu/home/baez/physics/Relativity/SR/acceleration.html) What difference is there between general and special, as long as the ship isn't traveling cosmological distances or near large masses?
- Also, the point of making the inertial legs of the trip long enough--or the acceleration at the U-turn large enough--is to let you work out the problem with just algebra, instead of calculus, by making the parts of the trip under acceleration a trivial fraction of the whole. You can't do that by making the acceleration small.
- —wwoods 06
- 32, 20 Nov 2004 (UTC)
spin proviso
On Sept 3 2004, Wodan asked about the quandry of spinning. If spinning is relativistically the same as being stock still while the entire cosmos whirls around about you, then that seems to allow for objcts to be moving at speeds far greater than lightspeed. But what Wodan is overlooking is the fact that in such a scenario (the entire cosmos whirling about you), no specific object is moving faster than lightspeed with respect to any other specific object. So Wodan has confused REAL relative motion with the purely human-concocted construct of moving with respect to a contrived hypothetical x-y-z frame; and those are quite disparate notions! There's no violation of the sanctity of lightspeed in perceiving the entire cosmos as whirling around that way. --ETP 13:34, 16 Dec 2004 (UTC)
dispensing with GR
As regards the question whether or not the TwinParadox can be resolved without GR, SR is just fine for all flat space purposes, including accelerations. I can show you a derivation that starts with the Lorentz Transform alone and ends up with the formula for gravitational clockrate differential, which is EQUIVALENT to acceleration-deduced clockrate differential, which is dt/dt'=(1+ax'/c^2)/gamma, where a is the g-force strength and x' is the distance to the remote clock, sign significant. You know what gamma is.
The Twin Paradox in SR boils down to the distortion inaptly termed... The Relativity of Simultaneity -- I'm sure you've all heard. I call it clock dissynchronicity. Yes, the Twin Paradox boils down to clock dissynchronicity and you might argue that time dilation is sorta inconsequential; but no, they all work in harmony. See also my "Twin Paradox resolved with Lorentz Transform alone" under External Links. --ETP 14:53, 16 Dec 2004 (UTC)
- It's not the twin paradox, in the ordinary usage of the phrase, if the twins aren't brought back to the same point — otherwise, it is meaningless to compare their ages because the answer depends on the frame of reference. (And the "need" for GR to explain the twin paradox was dispensed with over half a century ago.) —Steven G. Johnson 17:42, Dec 16, 2004 (UTC)
- <<the "need" for GR to explain the twin paradox was dispensed with over half a century ago>> That is perfectly true, but it was dispensed with from this Wikipedia article only a couple months ago, after much chatter. --ETP 01:58, 17 Dec 2004 (UTC)
- <<It's not the twin paradox, in the ordinary usage of the phrase>>
- Keyword: "ordinary". So think *outside* the box for a change: it's the timepiece that we're interested in, not the personalities. In my treatment, the timepiece is paramount, and the baton is passed at the halfway mark, with all due strict adherence to Relativity's constraints. The calculations are not flawed; the paradox is laid bare and then resolved, with elegance, lucidity and conciseness. If you doubt its utility, just show my essay to a bright seventeen-year old, and watch the enlightenment dawn.
- <<otherwise, it is meaningless to compare their ages because the answer depends on the frame of reference>>
- In that stated scenario of mine, there's only one right reckoning, true from ALL Frames-of-Ref, which is that Alf's clock will trail Terra's by 0.89 year, upon their coincidence. Look a bit harder and you'll see that. --ETP 02:31, 17 Dec 2004 (UTC)
Twins in a Periodic Spacetime
Nothing prevents a spatially periodic spacetime in special relativity. It still can be flat. No kidding. It's a boundary condition. It's interesting to consider the Twin Paradox under these circumstances, because the twins can be truly symmetric. That is, in a periodic spacetime, they can meet again without undergoing acceleration. I'm not certain about the resolution of the paradox in this case. However, the existence in a periodic spacetime of two different light cones connecting the twins, one forward and one back in a 1-D periodic space, may be a clue. -MFR
Re Alternative Resolution of Paradox
The section entitled "Alternative Resolution of Paradox", along with two depictions, was add 3/27/2005 by Cpcjr. Congratulations! It looks okay on the surface, but it fails to explain how the spaceship crew accounts for the Earthbound twin's time dilation during either leg. The answer lies in the fact that the deceleration and subsequent acceleration of the spacecraft at the distant star system more than compensates for said time dilation. To reiterate: if the spaceship crew ages only 2.57 years during the outbound leg, then why doesn't the Earthbound twin age only half that, or 1.28 years during that span, throwing off the entire explanation? Okay, maybe I'm just fond of splitting hairs... and I have NO intention of editting anything. But I will take this opportunity to tout my own very fine explanation, which makes no convenient omissions, and resolves the paradox using only the basic Lorentz Transform. Find a link to my mercifully brief essay under External Links, below the article. Hey, I've never claimed that my explanation is unique or that it breaks any new ground! no, it's just a real fine lucid, eloquent and simple resolution done without smoke and mirrors and leaving nothing to the imagination. ETP 16:21, 28 Mar 2005 (UTC)
- No, you're absolutely correct, the "solution" does not solve anything and should be removed. Regardless of the trip and stay times, in fact, lets just call them T1 and S1, the travelling twin "should see" his Earth-bound counterpart age less. Period. That's the whole idea of the paradox, one that is apparently missing from this "solution". I am going to remove. Maury 02:16, 11 Apr 2005 (UTC)
I agree that the alternative solution avoids the issue, because it doesn't address what the person on the moving spaceship "sees" when looking at the stationary twin. Thus, it should be deleted. I'm also going to delete ETP's link to his own "explanation", because as I explained above, he resolved the "paradox" by changing the question, which is equally besides the point here. —Steven G. Johnson 04:35, Apr 11, 2005 (UTC)
- Go ahead and be an intellectual bigot. No tyro is ever going to understand the paradox resolution without the simplest of all possible pertinent information: namely that there are precisely THREE, rather than TWO, special relativistic distortions encompassed in the basic Lorentz transform. Everyone has had heard about length contraction and time dilation, but few realize that clock dissynchronicity is the third distortion... and it isn't even a very difficult concept to grasp -- certainly not arithmetically so. So go ahead and barrage the reader with spacetime diagrams, which impart little if any elucidation to the uninitiated. See if I care!ETP 05:03, 11 Apr 2005 (UTC)
- (William M. Connolley 20:47, 11 Apr 2005 (UTC)) Hmm, well, let me say that I found the std explanation (the one that remains) really rather helpful and clear.
- Clock synchronization is a well documented "problem" that is encountered in any greater discussion on relativity. "Odd clock" problems are another common class of physical paradoxes as well, although they are typically combined with length contraction (ie, "close the doors when the ladder..."). I agree that another (or additional) explaination containing a disuccsion of clock problems is likely a good idea. However the remove portion did not clearly do this, nor did it address the problem at all. I don't see how anyone can consider this "intellectual bigotry". Nor do I understand why you think tyrants (tyro?) would be reading this... Maury 21:48, 11 Apr 2005 (UTC)
It is true that the original version of the alternative resolution did not address how each twin observed the other. A new version has been posted that corrects this defect. Thanks for pointing it out.
Geodesics and closing a loop
In the Usenet Physics FAQ discussion of the Twin paradox (http://www.physics.adelaide.edu.au/~dkoks/Faq/Relativity/SR/TwinParadox/twin_paradox.html), it is shown that the magnitude of the difference in proper time can be calculated in as many as four of five different ways, all producing the same answer.
I favor the most abstract approach, I favor the approach that uses considerations of geometry and symmetry only.
It is possible to account for the difference in proper time on the basis of the invariance of the space-time interval. From the formula for the space-time interval, the following formula can be given for the proper time of a traveller
- <math>d \tau ^2 = dt^2 - dx^2 - dy^2 - dz^2 <math>
This formula expresses an asymmetry: the laziest way to travel a year ahead in time is to just do nothing. You wait a year, and at the end of that, a full year has passed. Alternatively, you can fire up the thrusters of your space-craft, and you can take a longer path through space towards a rendez-vous with the traveller who only waits for a full year to pass. Working up many extra miles of traveling it will take less than a year, say, 11 months, to travel towards a point of rendez-vous with the traveller who is inertial.
The formula expresses that the traveller who remains in the same inertial frame throughout the journey represents some ground level as far as proper time is concerned, somewhat akin to zero Kelvin. No matter what happens, the clocks that are co-moving with a traveller who moves inertially all the time (and stays away from gravitation) are the first to reach the point of a year of proper time. There is no physics that can make a clock count more proper time than that, it is only possible to count less proper time than that, by deviating from moving along a geodesic of Minkowski space-time, by taking "a longer road" towards the rendez-vous point in space-time. The rendez-vous is essential, it closes a loop. Without closure of the loop there is no such thing as being "the first to have counted a year of proper time".
What needs to be calculated is the path-integral of the path that is taken, the path with respect to the inertial frame of reference of the traveller who does nothing.
Relativity does not explain why time and space are related in this way. What would a universe be like in which taking longer path corresponds to counting more proper time? --Cleon Teunissen | Talk 09:48, 13 Apr 2005 (UTC)
There is no absolute space
In Special Relativity, there is the upper limit of velocity: the speed of light. Likewise there is an upper limit in the rate of time.
A clock that moves inertially, and stays away from gravitation, is in step with time at its maximum rate. All clocks that take a longer path through space than the inertially moving clock, are seen to have been in step with time that proceeded at a slower rate than the maximum rate. So when clocks separate and later reunite at a point of rendez-vous, the "wandering" clock is seen to have counted, say, 11 months, instead of the 12 months of the clock that is in step with time-at-its-maximum-rate.
This does not in any way imply absolute space. The asymmetry in rate of time is subject only to difference in path length, relative to the inertial frame co-moving with the inertially moving traveller.
Still, there is an asymmetry. To focus on that asymmetry I use the following reasoning: all inertial frames are indistinguishable, so I might just as well envision a superposition of the entire group of all inertial frames of reference, and summerize that with the name the inertial frame of reference. I treat the entire symmetry-group of inertial frames of reference as effectively a single frame.
If two clocks separate and later rejoin, there is a loop. And whenever there is a loop, enclosing an area, at least one the the clocks has not moved along a geodesic, and in Minkowski space-time that matters: moving along a geodesic or not is different physics taking place. The geodesics of Minkowski space-time relate to the inertial frame of reference. Minkowski space-time is not a neutral background, it is not just empty space. Minkowski space-time is a physical entity that affects the rate of time of objects moving through it. --Cleon Teunissen | Talk 11:06, 13 Apr 2005 (UTC)
The Twin paradox and time dissemination
In the following discussion I shall use the names that the siblings have in the Usenet Physics FAQ. The twin who stays at home is called Terence, and the twin who travels into space is called Stella.
The essence of the Twin scenario is that it is a scenario of time dissemination. To see this, imagine a fleet of space-ships, travelling in interstellar space. The ships are cruising in formation (no relative velocity) so the clocks of all the ships count time at the same rate. They want a procedure to ensure all the clocks are synchronized. They can use radio-signals for that, in which case they need to take the transtion time of the radio-signals into account, or they can use a separate ship that visits the other ships one by one, disseminating time. Either with radio-signals or a portable clock, the transition time must be taken into account.
In the discussion of the Twin scenario in the Usenet Physics FAQ; Twin paradox (http://www.physics.adelaide.edu.au/~dkoks/Faq/Relativity/SR/TwinParadox/twin_paradox.html) the math is simplified by using the following scenario: at the point in space-time of separation Stella is in her spaceship, passing Earth at a constant velocity. At the point of closest approach to Earth she and Terence synchronize their clocks. It is the fact that they both set a clock to zero at a specific point in space-time that counts.
The physics of the Time disseminaton scenario does not require Stella to make a physical U-turn herself. The essence of the scenerio is preserved when another space-traveller, lets call her 'Allets', synchronizes her clock with the clock of Stella as she passes Stella, and after that Allets goes on to the point of rendez-vous, where she and Terence compare clock-readings.
In the Usenet Physcis FAQ Twin paradox discussion several calculations are presented, including a calculation based on instantaneous turnaround of Stella. That scenario is equivalent to a relay of Stella to Allets, with Allets synchronizing her clock with the clock of Stella at the moment that they pass each other.
This facilitates an interpretation of the Twin paradox in purely geometric terms.
In space, Allets retraces the (straight) path that Stella had taken moving away from Terence. In the space-time diagram, that looks like a triangle.
A remarkable feature of the geometry of time dissemination is that the difference in time at the point of rendez-vous is independent of the velocity of Stella and Allets. Suppose that the space journey is 300.000 kilometers out into space and back again. It would take radio signals 2 seconds to make that round trip and a time dissemination relay by space-travellers results at the point where the loop is closed in the same 2 seconds behind a traveller who has remained on Earth.
This independency on the travel velocity of the time dissemination relay can be seen in the space-time diagram. To focus on the most simple case, we put the point of separation somewhere in interstellar space, where the gravitation of surrounding suns cancels almost completely. Terence moves inertially, so his time is at maximum rate for his plane of simultaneity.
The space-time diagrams for different velocities of travel are different in shape, but in the end the difference in counted time is 2 seconds if the trip is 300.000 kilometers out into space. In terms of geometry this is Pythagoras' theorem. The slower the velocity of Stella and Allets in the time disseminaton relay, the more time it takes from separaton to reclosing the loop, but in the end the difference in proper time is always 2 seconds.
Relativistic physics does not explain why space and time are in this pythagorean relation to each other, it just describes it. --Cleon Teunissen | Talk 06:26, 18 Apr 2005 (UTC)
I just read what you (Cleon) wrote in the article and in the talk, e.g. A remarkable feature of the geometry of time dissemination is that the difference in time at the point of rendez-vous is independent of the velocity of Stella and Allets THIS IS FALSE I think you forgot the square root!!! The 300000 Km <-> 1 second of delay relation is true only for light, i.e. when
- <math>d s ^2 = 0 <math>
- Yeah, it has dawned on me now. It's nice round numbers only for light. It was too simple to be true. I shall have to rewrite. Some of it can remain, I think. The bit about showing how time dissemination procedure illustrates the principle of relativity of inertial motion, for example. I think that will, after proper rewrite, be usable. --Cleon Teunissen | Talk 17:21, 23 Apr 2005 (UTC)
There is no Paradox
...and you dont need General Relativity.
And it can be explained without complex calculations.
Consider a Ten Year Trip.
The observer on the Ship sees the earth receeding for 5 years and converging for 5 years.
The observer on earth sees the ship receeding for longer than five years because at the point he turns around light takes a long time to reach earth. The return journey seems a lot faster as from the earths viewpoint he is chasing his own light.
Now with two different times of visible receeding and converging we have two different results. Put them into standard special relativity calculations and no paradox exists.
At the point the ship switches intertial frames(turns around). He has a totally different view of when past events occured on earth.
- In the Twin paradox, one must distinguish between two kinds of suspicion: (1) Are we baffled because there is an inconsistency in the theoretical framework of relativistic physics? (2) The theory is self-consistent, but incomplete.
- Its number (2). The twins are traveling with portable atomic clocks and at the point of rendez-vous the clock of the twin who has travelled has counted less cycles. In the end all clocks, including biologial and mechanical clocks, measure rate of time because the underlying quantumprocesses happen in time. This shows that relativistic physics deals for a 100% with quantumbehavior. It is sometimes said that relativistic physics 'describes macroscopic phenomena' and that quantum physics 'describes the microscopic world of quantum particles', but the Twin paradox brings into focus the reality that quantumbehavior is affected by space-time geometry.
- In order to complete the theory a quantumphysical model would have to be found that predicts the physics of Minkowski space-time on the basis of more fundamental physics. --Cleon Teunissen | Talk 14:45, 29 Apr 2005 (UTC)