Star polygon
|
|
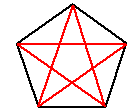
In geometry, a star polygon is a complex, regular polygon, so named for its starlike appearance, created by extending lines in a regular pattern from one vertex of a simple, regular, n-sided polygon to another, non-adjacent vertex and continuing the process until the original vertex is reached again. For instance, in a regular pentagon, a five-pointed star can be obtained by drawing a line from the first vertex to the third vertex, from the third vertex to the fifth vertex, from the fifth vertex to the second vertex, from the second vertex to the fourth vertex, and from the fourth vertex to the first vertex. This involves repeated addition with a modulus of n, where n is the number of sides of the polygon and the number x to be repeatedly added is greater than 1 and less than n-1, or: 1 < x < n-1. The notation for such a polygon is {n/x}. The polygon at right is {5/2}.
It is worth noting that if the modulus n is evenly divisible by x, the star polygon obtained will be a regular polygon with n/x sides. A complex star polygon can be obtained by rotating these regular n/x-gons one vertex to the left on the original polygon until the number of vertices rotated equals n/x minus one. An extreme case of this is that any instance where n is an even number and n/x is 2 produces a straight line, or a degenerate star polygon.
Star polygons can be thought of as diagramming cosets of the subgroups <math>x\mathbb{Z}_n<math> of the finite group <math>\mathbb{Z}_n<math>.
Star_polygon(8-3).png
Certain star polygons feature prominently in art and culture. These include:
- The {5/2} star polygon is known as a pentagram, pentacle or pentangle, and is considered by some to have occult significance;
- The {8/3} star polygon, and the complex star polygon of two {16/6} polygons, are frequent geometrical motifs in Mughal Islamic art and architecture;
- The complex {8/2} star polygon (i.e. two squares) is known as the Star of Lakshmi, and figures in Hinduism;
- The simplest non-degenerate complex star polygon is two {6/2} polygons (i.e., triangles), and is known as the Star of David (or sometimes, hexagram); and
- The {7/3} and {7/2} star polygons are known as heptagrams. They also have occult significance, for example in the Kabbalah and in Wicca.
- An eleven pointed stars is called a hendecagram.
The star polygons were first studied by Thomas Bradwardine.
External links
- Star Polygon -- from MathWorld (http://mathworld.wolfram.com/StarPolygon.html)de:Stern (Geometrie)