Braid group

In mathematics, the braid group on n strands, denoted by B_n, is a certain group which has a nice geometrical representation and in a sense generalizes the symmetric group S_n. Here, n is a natural number; if n > 1, then B_n is an infinite group.

Braid groups were introduced explicitly by Emil Artin in 1925, although (as Wilhelm Magnus pointed out in 1974) they were already implicit in Adolf Hurwitz's work on monodromy (1891). In fact, as Magnus says, Hurwitz gave the interpretation of a braid group as the fundamental group of a configuration space, an interpretation that was lost from view until it was rediscovered by Ralph Fox and Lee Neuwirth in 1962!

Contents

1 Intuitive description 2 Generators and relations 3 Relation to the symmetric group, group actions 4 Some properties 5 Computational aspects 6 Formal treatment 7 See also

Intuitive description

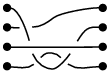
For this introduction, we will take n=4; the generalization to other values of n will be straightforward. Consider two sets of four items lying on a table, with the items in each set being arranged in a vertical line, and such that one set sits next to the other. (In the illustrations below, these are the black dots.) You are given four strands, and you are to connect each item of the first set with an item of the second set so that a one-to-one correspondence results. Such a connection we call a braid. Often some strands will have to pass over or under others, and this is crucial: the following two connections are different braids:

is different from

Missing image Braid_s1.png The braid sigma_1

On the other hand, two such connections which can be made to look the same by "pulling the strands" are considered the same braid:

is the same as

We require that all strands move from left to right; knots like the following are not considered braids:

is not a braid

Now given two braids, we can compose them by drawing the first next to the second, identifying the four items in the middle, and connecting corresponding strands:

composed with

yields

Missing image Braid_s3s2.png image:braid_s3s2.png

Another example:

Missing image Braid_s1_inv_s3_inv.png image:braid_s1_inv_s3_inv.png

composed with

Missing image Braid_s1_s3_inv.png image:braid_s1_s3_inv.png

yields

The composition of the braids σ and τ is written as στ.

The set of all braids on four strands is denoted by B₄. The above composition of braids is indeed a group operation. The neutral element is the braid consisting of four parallel horizontal strands, and the inverse of a braid consists of that braid which "undoes" whatever the first braid did. (Our first two example braids above are inverses of each other.)

Generators and relations

Consider the following three braids:

Missing image Braid_s1.png image:braid_s1.png
σ1	σ2	σ3

It turns out that every braid can be written as a composition of a number of these braids and their inverses. In other words, these three braids generate the group B₄. To see this, take an arbitrary braid and scan it from left to right; whenever you encounter a crossing of strand i and i+1 (counting from the top), write down σ_i or σ_i^-1, depending on whether strand i moves under or over strand i+1. When you reach the right end, you have written your braid as a product of the σ's and their inverses.

It's clear that

σ₁σ₃ = σ₃σ₁.

The following two relations are not quite as obvious:

σ₁σ₂σ₁ = σ₂σ₁σ₂

σ₂σ₃σ₂ = σ₃σ₂σ₃

(Verify these on a piece of paper!)

One can show that all other relations among the braids σ₁, σ₂ and σ₃ already follow from these relations and the group axioms.

So one can abstractly define the group B_n via the following presentation:

• generators σ₁,...,σ_n-1
• relations (known as the braid relations):
  • σ_i σ_j = σ_j σ_i whenever |i -j| ≥ 2 ;
  • σ_i σ_i+1 σ_i = σ_i+1 σ_i σ_i+1 for i = 1,..., n-2

Relation to the symmetric group, group actions

Every braid on n strands basically consists of a one-to-one correspondence between two sets of n items, and some topological information about how the strands establish this correspondence. If we forget this topological information, then every braid yields a one-to-one correspondence of n items; these are precisely the elements of the symmetric group S_n. It turns out that this assignment is in fact a surjective group homomorphism B_n → S_n.

The kernel of this group homomorphism is called the pure Braid group on n strands; intuitively, it consists of those braids which connect the i-th item of the left set to the i-th item of the right set, for all i.

The symmetric group S_n has a very similar presentation to the one given above: if you take the braid relations and add the relations

σ_i² = 1 for i=1,...,n-1

then you obtain a presentation for S_n (the σ_i can then be thought of as transpositions of two neighboring elements).

One frequently encounters a situation where n items are being permuted "up to a twist", and then there is often an underlying group action of a braid group. As a prototypical example, consider an arbitrary group G and the set X of all n-tuples of elements of G whose product is 1. Then B_n operates on X in a natural fashion: given a tuple x = (x₁,...,x_n) in X, we define σ_i.x = (x₁,...,x_i-1,x_i+1,x_i+1^-1x_ix_i+1,x_i+2,...,x_n). This operation satisfies the braid relations and thus defines a group action of B_n on X.

Some properties

The groups B₀ and B₁ are trivial; B₂ is already infinite and isomorphic to the infinite cyclic group Z. B₃ is a quite complicated non-abelian infinite group.

In general, B_n is a subgroup of B_n+1: it can be viewed as consisting of all those braids on n+1 strands in which the bottom strand is horizontal and does not cross nor is crossed by any other strand.

So in particular, B_n is abelian if and only if n ≤ 2.

There is a useful notion of "length" for the elements of the Braid group, given by the group homomorphism w : B_n → Z that maps every σ_i to 1.

Computational aspects

The word problem for the braid relations is efficiently solvable and there exists a normal form for elements of B_n in terms of the generators σ₁,...,σ_n−1. (In essence, computing the normal form of a braid is the algebraic analogue of "pulling the strands" as illustrated in our second set of images above.) The free GAP computer algebra system can carry out computations in B_n if the elements are given in terms of these generators. There is also a package called CHEVIE for GAP3 with special support for braid groups.

Since there are nevertheless several hard computational problems about braid groups, applications in cryptography have been suggested.

Through cutting, every knot and every link can be represented by a braid (see Alexander's theorem in braid theory). Since braids can be concretely given as words in the σ_i, this is often the preferred method to enter knots into computer programs.

Formal treatment

To put the above informal discussion of braid groups on firm ground, one needs to use the homotopy concept of algebraic topology. This is outlined in the article on braid theory.

Alternatively, one can eschew topology altogether and define the braid group purely algebraically via the braid relations.

See also

• representation theory of the braid group