Skein relation
|
|
Skein relations occur in knot theory, where they are most often used to give a simple definition of a knot polynomial. Informally, a skein relation gives a linear relation between the values of a knot polynomial on a collection of links which differ from each other only in a small region. For some knot polynomials, such as the Conway, Alexander, and Jones polynomials, the relevant skein relations are sufficient to calculate the polynomial recursively. For others, such as the HOMFLYPT polynomial, more complicated algorithms are necessary.
More formally, a skein relation should be thought of as defining the kernel of a quotient map from the planar algebra of tangles. Such a map corresponds to a knot polynomial if all closed diagrams are taken to some (polynomial) multiple of the image of the empty diagram.
Depending on the knot polynomial in question, the links (or tangles) appearing in a skein relation may be oriented or unoriented.
Given three link diagrams that are identical except for one crossing, the three are labelled as follows. Turn the diagrams so the directions at that spot are both roughly northward. One diagram will have northwest over northeast, it is labelled L-. Another will have northeast over northwest, it's L+. The remaining diagram is lacking that crossing and is labelled L0.
- Missing image
Skein-relation-patches.png
image:skein-relation-patches.png
(The labelling is actually independent of direction insofar as it remains the same if all directions are reversed. Thus polynomials on undirected knots are unambiguously defined by this method. However, the directions on links are a vital detail to retain as one recurses through a polynomial calculation.)
It is also sensible to think in a generative sense, by taking an existing link diagram and "patching" it to make the other two—just so long as the patches are applied with compatible directions.
To recursively define a knot (link) polynomial, a function F is fixed and for any triple of diagrams and their polynomials labelled as above,
- <math>F(L_-,L_0,L_+)=0<math>
or more pedantically
- <math>F\Big(L_-(x),L_0(x),L_+(x),x\Big)=0<math> for all x
(Finding an F which produces polynomials independent of the sequences of crossings used in a recursion is no trivial exercise.)
Example
Sometime in the early '60s, Conway showed how to find Alexander polynomials using skein relations. As a recursion, it is not quite so direct as the matrix method; on the other hand, parts of the work done for one knot will apply to others. In particular, the network of diagrams is the same for all skein-related polynomials.
Let function P from diagrams to Laurent series in <math>\sqrt x<math> be such that <math>P({\rm unknot})=1<math> and a triple of skein-relation diagrams <math>(D_-, D_0, D_+)<math> satisfies the equation
- <math>P(D_-) = (x^{-1/2}-x^{1/2})P(D_0) + P(D_+)<math>
Then P maps a knot to one of its Alexander polynomials.
The example is a working of the cinquefoil knot. For convenience, let A = x−1/2−x1/2. Patch one of its crossings so:
- P(
) = A × P(Missing image
Skein-relation-cinquefoil-zero-sm.png
image:skein-relation-cinquefoil-zero-sm.png
) + P(
)
The first diagram is actually a trefoil; the second diagram is two unknots with four crossings. Patching the latter
- P(
) = A × P(Missing image
Skein-relation-link24-zero-sm.png
image:skein-relation-link24-zero-sm.png
) + P(Missing image
Skein-relation-link24-plus-sm.png
image:skein-relation-link24-plus-sm.png
)
gives, again, a trefoil, and two unknots with two crossings. Patching the trefoil
- P(
) = A × P(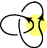
) + P(Missing image
Skein-relation-trefoil-plus-sm.png
image:skein-relation-trefoil-plus-sm.png
)
gives that 2-crossing link and the unknot. Patching that link
- P(Missing image
Skein-relation-link22-minus-sm.png
image:skein-relation-link22-minus-sm.png
) = A × P(Missing image
Skein-relation-link22-zero-sm.png
image:skein-relation-link22-zero-sm.png
) + P(Missing image
Skein-relation-link22-plus-sm.png
image:skein-relation-link22-plus-sm.png
)
gives a link with 0 crossings. That takes a bit of sneakiness:
- P(
) = A × P(Missing image
Skein-relation-link20-zero-sm.png
image:skein-relation-link20-zero-sm.png
) + P(Missing image
Skein-relation-link20-plus-sm.png
image:skein-relation-link20-plus-sm.png
)
We now have enough relations to compute the polynomials:
| knot name | diagram(s) | P(diagram) | ||
|---|---|---|---|---|
| eq'n | abbr'd | in full | ||
| unknot |  Missing imageSkein-relation-link20-plus-sm.png image:skein-relation-link20-plus-sm.png Missing image Skein-relation-link22-zero-sm.png image:skein-relation-link22-zero-sm.png  | 1 | x→1 | |
| Missing image Skein-relation-link20-zero-sm.png image:skein-relation-link20-zero-sm.png Missing image Skein-relation-link22-minus-sm.png image:skein-relation-link22-minus-sm.png | 1=A?+1 | 0 | x→0 | |
| (Hopf link)[1] (http://mathworld.wolfram.com/HopfLink.html) | Missing image Skein-relation-link22-plus-sm.png image:skein-relation-link22-plus-sm.png  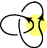 | 0=A1+? | -A | x→x1/2-x-1/2 |
| trefoil | Missing image Skein-relation-link24-zero-sm.png image:skein-relation-link24-zero-sm.png Missing image Skein-relation-trefoil-plus-sm.png image:skein-relation-trefoil-plus-sm.png  | 1=A(-A)+? | 1+A2 | x→x-1-1+x |
| Missing image Skein-relation-link24-plus-sm.png image:skein-relation-link24-plus-sm.png Missing image Skein-relation-cinquefoil-zero-sm.png image:skein-relation-cinquefoil-zero-sm.png | -A=A(1+A2)+? | -A(2+A2) | x→-x-3/2+x-1/2-x1/2+x3/2 | |
| cinquefoil |  | 1+A2=A(-A(2+A2))+? | 1+3A2+A4 | x→x-2-x1+1-x+x2 |
Hints:
- A = (1 − x)/x1/2
- A2 = (1 − 2x + x2)/x
- A3 = (1 − x)3/x3/2 = (1 − 3x + 3x2 − x3)/x3/2
- A4 = (1 − x)4/x2 = (1 − 4x + 6x2 − 4x3 + x4)/x2
External links
- AMS (http://www.ams.org/new-in-math/cover/knots3.html)
- Mathworld (http://mathworld.wolfram.com/SkeinRelationship.html)
- HOMFLY polynomial of decorated Hopf link (http://arxiv.org/abs/math.GT/0108011)