Interval (music)
|
|
In music theory, an interval is the distance in pitch between two notes, the lower and higher members of the interval. It often refers to those two notes themselves (otherwise known as a dyad). Larger intervals are described as wide and smaller ones as narrow, but these are only relative terms.
Intervals may occur two ways:
- vertical (or harmonic) if the two notes sound simultaneously
- linear (or melodic), if the notes sound successively.
An interval class is an interval measured by the shortest distance possible between its two pitch classes.
| Contents |
Frequency ratios
In just intonation intervals are commonly labelled according to the ratio of frequencies of the two pitches. Important intervals are those using the lowest integers, such as 1/1, 2/1, 3/2, etc. This system is frequently used to describe intervals in non-Western music. This method is also often used in theoretical explanations of equal-tempered intervals used in European tonal music which explain their use through their approximation of just intervals.
Interval number and quality
In diatonic or tonal theory intervals are labelled according to their diatonic function and according to the number of members or degrees they span in a diatonic scale.
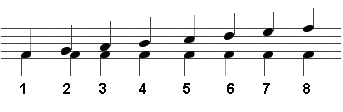
The interval number of a note from a given tonic note is the number of staff positions enclosed within the interval, as shown at right. Intervals larger than an octave are called compound intervals; for example, a tenth is known as a compound third. Intervals larger than a thirteenth are rarely spoken of (but see 8va for use of 15ma).
The name of any interval is further qualified using the terms perfect, major, minor, augmented, and diminished. This is called its interval quality.
- Unison, fourth, fifth, octave. These intervals may be perfect, augmented, or diminished. A perfect fourth is five semitones, a perfect fifth is seven semitones, a perfect octave is twelve semitones. A perfect unison occurs between notes of the same pitch, so it is zero semitones. In each case, an augmented interval contains one more semitone, a diminished interval one fewer.
- Second, third, sixth, seventh. These intervals may be major, minor, augmented, or diminished.
- Major seconds are two semitones, also called a whole step, minor seconds are one semitone, also called a half step.
- Major thirds are four semitones, minor thirds are three semitones.
- Major sixths are nine semitones, minor sixths are eight semitones.
- Major sevenths are eleven semitones, minor sevenths are ten semitones.
- In each case, the augmented interval contains one semitone more than the major interval, and the diminished interval one semitone fewer than the minor interval.
It is possible to have doubly-diminished and doubly-augmented intervals, but these are quite rare.
Shorthand notation
Intervals are often abbreviated with a P for perfect, m for minor, M for major, d for diminished, A for augmented, followed by the diatonic interval number. The octave is P8, and a unison is usually referred to simply as "a unison" but can be labeled P1. The tritone, an augmented fourth or diminished fifth is often π or TT. Examples:
- m2: minor second
- M3: major third
- P5: perfect fifth
- m9: minor ninth
Enharmonic intervals
Two intervals are considered to be enharmonic if they both contain the same pitches spelled in different ways; that is, if the notes in the two intervals are enharmonic with one another. Enharmonic intervals contain the same number of semitones. For example C#-D#, a major second, and C#-Eb, a diminished third, are enharmonic.
Steps and skips
Linear (melodic) intervals may be described as steps or skips in a diatonic context. Steps are linear intervals between consecutive scale degrees while skips are not, although if one of the notes is chromatically altered so that the resulting interval is three semitones or more (e.g. C to D sharp), that may also be considered a skip. However, the reverse is not true: a diminished third, an interval comprising two semitones, is still considered a skip.
The words conjunct and disjunct refer to melodies composed of steps and skips, respectively.
Pitch class intervals
Post-tonal or atonal theory, originally developed for equal tempered European classical music written using the twelve tone technique or serialism, integer notation is often used, most prominently in musical set theory. In this system intervals are named according to the number of half steps, from 0 to 11, the largest interval class being 6.
Ordered and unordered pitch and pitch class intervals
In atonal or musical set theory there are numerous types of intervals, the first being ordered pitch interval, the distance between two pitches upward or downward. For instance, the interval from C to G upward is 7, but the interval from G to C downward is −7. One can also measure the distance between two pitches without taking into account direction with the unordered pitch interval, somewhat similar to the interval of tonal theory.
The interval between pitch classes may be measured with ordered and unordered pitch class intervals. The ordered one, also called directed interval, may be considered the measure upwards, which, since we are dealing with pitch classes, depends on whichever pitch is chosen as 0. For unordered pitch class interval see interval class.
Generic and specific intervals
In diatonic set theory, specific and generic intervals are distinguished. Specific intervals are the interval class or number of semitones between scale degrees or collection members, and generic intervals are the number of scale steps between notes of a collection or scale.
Cents
The standard system for comparing intervals of different sizes is with cents. This is a logarithmic scale in which the octave is divided into 1200 equal parts. In equal temperament, each semitone is exactly 100 cents.
Comparison of different interval naming systems
| # semitones | Interval class | Generic interval | Common diatonic name | Comparable just interval | Comparison of interval width in cents | ||
| equal temperament | just intonation | quarter-comma meantone | |||||
| 0 | 0 | 0 | perfect unison | 1:1 | 0 | 0 | 0 |
| 1 | 1 | 1 | minor second | 16:15 | 100 | 112 | 117 |
| 2 | 2 | 1 | major second | 9:8 | 200 | 204 | 193 |
| 3 | 3 | 2 | minor third | 6:5 | 300 | 316 | 310 |
| 4 | 4 | 2 | major third | 5:4 | 400 | 386 | 386 |
| 5 | 5 | 3 | perfect fourth | 4:3 | 500 | 498 | 503 |
| 6 | 6 | 3 4 | augmented fourth diminished fifth | 45:32 64:45 | 600 | 590 610 | 579 621 |
| 7 | 5 | 4 | perfect fifth | 3:2 | 700 | 702 | 697 wolf fifth 737 |
| 8 | 4 | 5 | minor sixth | 8:5 | 800 | 814 | 814 |
| 9 | 3 | 5 | major sixth | 5:3 | 900 | 884 | 889 |
| 10 | 2 | 6 | minor seventh | 16:9 | 1000 | 996 | 1007 |
| 11 | 1 | 6 | major seventh | 15:8 | 1100 | 1088 | 1083 |
| 12 | 0 | 0 | perfect octave | 2:1 | 1200 | 1200 | 1200 |
It is possible to construct just intervals which are closer to the equal-tempered equivalents, but most of the ones listed above have been used historically in equivalent contexts. In particular the tritone (augmented fourth or diminished fifth), could have other ratios; 17:12 (603 cents) is fairly common. The 7:4 interval has been a contentious issue throughout the history of music theory; it is 31 cents flatter than a minor seventh. Some assert the 7:4 is one of the blue notes used in jazz.
The diatonic intervals, as well, have other enharmonic equivalents, such as augmented second for minor third.
Consonant and dissonant intervals
Consonance and dissonance are relative terms referring to the stability, or state of repose, of particular musical effects. Dissonant intervals would be those which cause tension and desire to be resolved to consonant intervals.
These terms are relative to the usage of different compositional styles.
- In atonal music all intervals (or interval classes) are considered equally consonant melodically and harmonically.
- In the middle ages, only the octave and perfect fifth were considered consonant harmonically.
- In 16th-century usage, perfect fifths and octaves, and major and minor thirds and sixths were considered harmonically consonant, and all other intervals dissonant. In the common practice period, it makes more sense to speak of consonant and dissonant chords, and certain intervals previously thought to be dissonant (such as minor sevenths) became acceptable in certain contexts. However, 16th-century practice continued to be taught to beginning musicians throughout this period.
- Hermann von Helmholtz (1821-1894) defined a harmonically consonant interval as one in which the two pitches have an overtone in common (specifically excluding the seventh harmonic). This essentially defines all seconds and sevenths as dissonant, and perfect fourths and fifth, and major and minor thirds and sixths, as consonant.
- Pythagoras defined a hierarchy of consonance based on how small the numbers were which express the ratio. 20th-century composer and theorist Paul Hindemith's system has a hierarchy with the same results as Pythagoras's, but defined by fiat rather than by interval ratios, to better accommodate equal temperament, all of whose intervals (except the octave) would be dissonant using acoustical methods.
- David Cope (1997, p.40-41) suggests the concept of interval strength, in which an interval's strength, consonance, or stability is determined by its approximation to a lower and stronger, or higher and weaker, position in the harmonic series. See also: Lipps-Meyer law.
All of the above analyses refer to vertical (simultaneous) intervals.
Inversion
An interval may be inverted, by raising the lower pitch an octave, or lowering the upper pitch an octave (though it is less usual to speak of inverting unisons or octaves). For example, the fourth between a lower C and a higher F may be inverted to make a fifth, with a lower F and a higher C. Here are the ways to identify interval inversions:
- For diatonically-named intervals, here are two rules, applying to all simple (i.e., non-compound) intervals:
- The number of any interval and the number of its inversion always add up to nine (four + five = nine, in the example just given).
- The inversion of a major interval is a minor interval (and vice versa); the inversion of a perfect interval is also perfect; the inversion of an augmented interval is a diminished interval (and vice versa); and the inversion of a double augmented interval is a double diminished interval (and vice versa).
- A full example: E flat below and C natural above make a major sixth. By the two rules just given, C natural below and E flat above must make a minor third.
- For intervals identified by ratio, the inversion is determined by reversing the ratio and multiplying by 2. For example, the inversion of a 5:4 ratio is an 8:5 ratio.
- Intervals identified by integer can be simply subtracted from 12. However, since an interval class is the lower of the interval integer or its inversion, interval classes cannot be inverted.
Interval roots
Although intervals are usually designated in relation to their lower note, David Cope and Hindemith both suggest the concept of interval root. To determine an interval's root, one locates its nearest approximation in the harmonic series. The root of a perfect fourth, then, is its top note because it is an octave of the fundamental in the hypothetical harmonic series. The bottom note of every odd diatonically numbered intervals are the roots, as are the tops of all even numbered intervals. The root of a collection of intervals or a chord is thus determined by the interval root of its strongest interval.
As to its usefulness, Cope provides the example of the final tonic chord of some popular music being traditionally analyzable as a "submediant six-five chord" (added sixth chords by popular terminology), or a first inversion seventh chord (possibly the dominant of the mediant V/iii). According the interval root of the strongest interval of the chord (in first inversion, CEGA), the perfect fifth (C-G), is the bottom C, the tonic.
Interval cycles
Interval cycles, "unfold a single recurrent interval in a series that closes with a return to the initial pitch class", and are notated by George Perle using the letter "C", for cycle, with an interval class integer to distinguish the interval. Thus the diminished seventh chord would be C3 and the augmented triad would be C4. A superscript may be added to distinguish between transpositions, using 0-11 to indicate the lowest pitch class in the cycle. (Perle 1990, p.21)
Other intervals
There are also a number of intervals not found in the chromatic scale or labeled with a diatonic function which have names of their own. Many of these intervals describe small discrepancies between notes tuned according to the tuning systems used. Most of the following intervals may be described as microtones.
- A Pythagorean comma is the difference between twelve justly tuned perfect fifths and seven octaves. It is expressed by the frequency ratio 531441:524288, and is equal to 23.46 cents
- A syntonic comma is the difference between four justly tuned perfect fifths and two octaves plus a major third. It is expressed by the ratio 81:80, and is equal to 21.51 cents
- A Septimal comma is 64/63, and is the difference between the Pythagorean or 3-limit "7th" and the "harmonic 7th".
- Diesis is generally used to mean the difference between three justly tuned major thirds and one octave. It is expressed by the ratio 128:125, and is equal to 41.06 cents. However, it has been used to mean other small intervals: see diesis for details
- A schisma (also skhisma) is the difference between five octaves and eight justly tuned fifths plus one justly tuned major third. It is expressed by the ratio 32805:32768, and is equal to 1.95 cents. It is also the difference between the Pythagorean and syntonic commas.
- A schismic major third is a schisma different than a just major third, eight fifths down and five octaves up, Fb in C.
- A quarter tone is half the width of a semitone, which is half the width of a whole tone.
- A kleisma is six major thirds up, five fifths down and one octave up, or, more commonly, 225:224.
- A limma is the ratio 256:243, which is the semitone in Pythagorean tuning.
- A ditone is the pythagorean ratio 81:64, two 9:8 tones.
- Additionally, some cultures around the world have their own names for intervals found in their music. See: sargam, Bali
Sources
- Cope, David (1997). Techniques of the Contemporary Composer, p.40-41. New York, New York: Schirmer Books. ISBN 0028647378.
- Perle, George (1990). The Listening Composer. California: University of California Press. ISBN 0520069919.
External links
- Tonalsoft Encyclopaedia of Tuning (http://tonalsoft.com/enc/index2.htm?interval.htm)de:Intervall (Musik)
eo:Intervalo (muziko) fr:Intervalle (musique) ko:음정 id:Interval it:Intervallo (musica) he:טון (מוזיקה) lv:Intervāls (mūzika) nl:Interval (muziek) ja:音程 pl:Interwał ru:Интервал (музыка) zh:音程