Maxwell-Boltzmann distribution
|
|
The Maxwell-Boltzmann distribution is a probability distribution with applications in physics and chemistry. It forms the basis of the kinetic theory of gases, which explains many fundamental gas properties, including pressure and diffusion. The Maxwell-Boltzmann distribution is also applied in electron transport and other phenomena. The Maxwell-Boltzmann distribution can apply to a number of related properties of the individual molecules in a gas. It is usually thought of as the distribution of molecular energies in a gas, but it can also refer to the distribution of velocities, speeds, momenta, and magnitude of the momenta of the molecules, each of which will have a different function describing the distribution, all of which are related. Also it may be expressed as a discrete distribution over a number of discrete energy levels, or as a continuous distribution over a continuum of energy levels.
The Maxwell-Boltzmann distribution can be derived using statistical mechanics (see the derivation of the partition function). As an energy distribution, it corresponds to the most probable energy distribution, in a collisionally-dominated system consisting of a large number of non-interacting particles in which quantum effects are negligible. Since interactions between the molecules in a gas are generally quite small, the Maxwell-Boltzmann distribution provides a very good approximation of the conditions in a gas.
In many other cases, however, the condition of elastic collisions dominating all other processes is not even approximately fulfilled. That is true, for instance, for the physics of the ionosphere and space plasmas where recombination and collisional excitation (i.e. radiative processes) are of far greater importance: in particular for the electrons. Not only would the assumption of a Maxwell distribution yield quantitatively wrong results, but even prevent a correct qualitative understanding of the physics involved. Also, in cases where the quantum thermal wavelength of the gas is not small compared to the distance between particles, there will be deviations from the Maxwell distribution due to quantum effects.
The Maxwell-Boltzmann energy distribution can be expressed as a discrete energy distribution by:
- <math>
\frac{N_i}{N} = \frac{\exp\left(-E_i/kT \right) } { \sum_{j}^{} {\exp\left(-E_j/kT\right)} } \qquad\qquad (1)<math>
where Ni is the number of molecules at equilibrium temperature T, in energy level i which has energy Ei, N is the total number of molecules in the system and k is the Boltzmann constant. (Note that sometimes the above equation is written with a factor gi denoting the degeneracy of energy states. In this case the sum will be over all energies, rather than all states.) Because velocity and speed are related to energy, Equation 1 can be used to derive relationships between temperature and the speeds of molecules in a gas. The denominator in this equation is known as the canonical partition function.
| Contents |
The Maxwell-Boltzmann distribution
The distribution of the momentum vector
What follows is a derivation wildly different from the derivation described by James Clerk Maxwell and later described with fewer assumptions by Ludwig Boltzmann.
For the case of an "ideal gas" consisting of non-interacting atoms in the ground state, all energy is in the form of kinetic energy. The relationship between kinetic energy and momentum for massive particles is
- <math>
E=\frac{p^2}{2m} <math>
where p2 is the square of the momentum vector p = [px, py, pz]. We may therefore rewrite Equation 1 as:
- <math>
\frac{N_i}{N} = \frac{1}{Z} \exp \left[ \frac{-(p_x^2 + p_y^2 + p_z^2)}{2mkT} \right] \qquad\qquad (3) <math>
where Z is the partition function, corresponding to the denominator in Equation 1. Here m is the molecular mass of the gas, T is the thermodynamic temperature and k is the Boltzmann constant. This distribution of Ni/N is proportional to the probability density function fp for finding a molecule with these values of momentum components, so:
- <math>
f_\mathbf{p} (p_x, p_y, p_x) = \frac{c}{Z} \exp \left[ \frac{-(p_x^2 + p_y^2 + p_z^2)}{2mkT} \right] \qquad\qquad (4)<math>
The normalizing constant c, can be determined by recognizing that the probability of a molecule having any momentum must be 1. Therefore the integral of equation 4 over all px, py, and pz must be 1.
It can be shown that:
- <math>
\int_{-\infty}^\infty \int_{-\infty}^\infty \int_{-\infty}^\infty \frac{1}{Z} \exp \left[ \frac{-(p_x^2 + p_y^2 + p_z^2)}{2mkT} \right]\,dp_x \, dp_y\,dp_z = \frac{1}{Z} \left( 2\pi m kT \right)^{3/2} \qquad\qquad (5)<math>
so in order for the integral of equation 4 to be 1,
- <math>
c = \frac{Z}{(\sqrt{2 \pi mkT}) ^ 3} \qquad\qquad (6)<math>
Substituting Equation 6 into Equation 4 and using pi = mvi for each component of momentum gives:
- <math>
f_\mathbf{p} (p_x, p_y, p_x) = \sqrt{\left( \frac{1}{2 \pi mkT} \right)^3} \exp \left[ \frac{-(p_x^2 + p_y^2 + p_z^2)}{2mkT} \right] \qquad\qquad (7)<math>
Distribution of the velocity vector
Recognizing that the velocity probability density fv is proportional to the momentum probability density function by
- <math>
f_\mathbf{v} d^3v = f_\mathbf{p} \left(\frac{dp}{dv}\right)^3 d^3v <math>
and using p=mv we get:
- <math>
f_\mathbf{v} (v_x, v_y, v_z) = \sqrt{ \left(\frac{m}{2 \pi kT} \right)^3} \exp \left[ \frac{-m(v_x^2 + v_y^2 + v_z^2)}{2kT} \right] \qquad\qquad (8)<math>
Which is the Maxwell-Boltzmann velocity distribution. The probability of finding a particle with velocity in the infinitesimal element [dvx, dvy, dvz] about velocity v = [vx, vy, vz] is
- <math>
f_\mathbf{v} \left(v_x, v_y, v_z\right) dv_x dv_y dv_z <math>
Distribution of the magnitude of momentum
We can find the distribution of the magnitude of the momentum by integrating
- <math>
f_p =\int_{\theta=0}^{\pi} \int_{\phi=0}^{2\pi}~ f_\mathbf{p} p^2 \sin(\theta)\,d\theta\, d\phi=4\pi\sqrt{\left( \frac{1}{2 \pi mkT} \right)^3}~p^2 \exp \left[\frac{-p^2}{2mkT}\right] <math>
Distribution of the energy
Finally, using p2 = 2mE we get the energy distribution:
- <math>
f_E=f_p\left(\frac{dp}{dE}\right)\,dE =2\sqrt{\frac{E}{\pi(kT)^3}}~\exp\left[\frac{-E}{kT}\right] <math>
The Maxwell-Boltzmann distribution can also be derived by considering it to be a quantum gas.
Velocity distribution in one direction
The Maxwell-Boltzmann velocity distribution for the vector velocity [vx, vy, vz] is the product of the distributions for each of the three directions:
- <math>
f_v \left(v_x, v_y, v_z\right) = f_v (v_x)f_v (v_y)f_v (v_z) <math>
where the distribution for a single direction is:
- <math>
f_v (v_i) = \sqrt{\frac{m}{2 \pi kT}} \exp \left[ \frac{-mv_i^2}{2kT} \right] \qquad\qquad (9)<math>
This distribution has the form of a normal distribution. As expected for a gas at rest, the average velocity in any particular direction is zero.
Distribution of speeds
Usually, we are more interested in the speed of molecules rather than the component velocities, where the speed, v is defined as:
- <math>
v = \sqrt{v_x^2 + v_y^2 + v_z^2} \qquad\qquad (10)<math>
The speed will therefore always be greater than or equal to zero. Since the v i are all normally distributed, it follows that v2 will be chi-square distributed with three degrees of freedom. If f(v) is the probability density function for the speed, then:
- <math>
f\left(v\right)dv = P(\chi^2|3)d\chi^2 <math>
where
- <math>
\chi^2 = \frac{mv^2}{kT} <math>
The probability density function for the speed is thus:
- <math>
f(v) dv = 4 \pi v^2 \left( \frac{m}{2 \pi kT} \right)^{3/2} \exp \left( \frac{-mv^2}{2kT} \right) dv \qquad\qquad (11)<math>
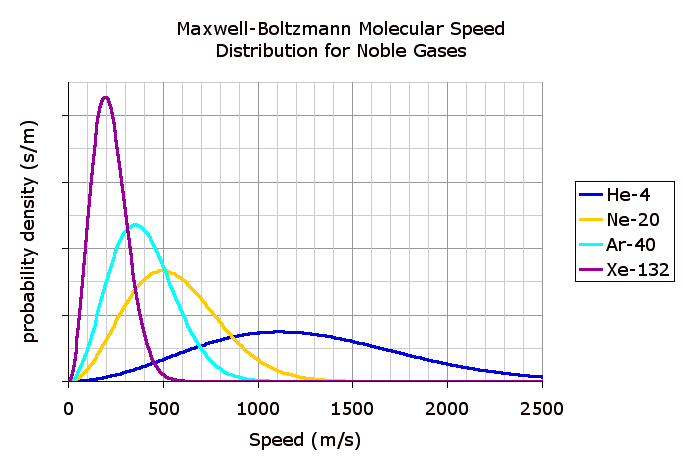
The following is a chart displaying the speed probability density functions for a few noble gases at a temperature of 298.15K (25 C).
Typical speed
Although Equation 11 gives the distribution of speeds or in other words the fraction of molecules having a particular speed, we are often more interested in quantities such as the average speed of the particles rather than the actual distribution. In the following subsections we will define and derive the most probable speed, the mean speed and the root-mean-square speed.
Most probable speed
The most probable speed, vp, is the speed most likely to be possessed by any molecule in the system and corresponds to the maximum value or mode of f(v). To find it, we calculate df/dv, set it to zero and solve for v:
- <math>\frac{df(v)}{dv} = \left( \frac{m}{2 \pi kT} \right)^{3/2} \exp \left( -mv^2/2kT \right) \left[ 8\pi v + 4 \pi v^2 (-mv/kT) \right] = 0\qquad\qquad (12)<math>
- <math>v_p = \sqrt { \frac{2kT}{m} } = \sqrt { \frac{2RT}{M} } \qquad\qquad (13)<math>
Mean speed
- <math> \langle v \rangle = \int_0^{\infin} v \, f(v) \, dv \qquad\qquad (14)<math>
Substituting for f(v) and performing the integration, we get
- <math> \langle v \rangle = \sqrt { \frac{8kT}{\pi m} } = \sqrt { \frac{8RT}{\pi M} } \qquad\qquad (15) <math>
Root-mean-square speed
The root mean square speed, vrms is given by
- <math>v_\mathrm{rms} = \sqrt{\int v^2 \, f(v) \, dv}. \qquad\qquad (16) <math>
Substituting for f(v) and performing the integration, we get
- <math>v_\mathrm{rms} = \sqrt { \frac{3kT}{m} } = \sqrt { \frac{3RT}{M} } \qquad\qquad (17)<math>
Thus,
- <math> v_p < \langle v \rangle < v_\mathrm{rms}. <math>de:Maxwell-Boltzmann-Verteilung
he:התפלגות מקסוול בולצמן nl:Maxwell-Boltzmann-verdeling ja:マクスウェル分布 pl:Rozkład Maxwella-Boltzmanna sl:Boltzmannova porazdelitev