List of moments of inertia
|
|
The following is a list of moments of inertia.
Moments of inertia
Moments of inertia have units of dimension mass × length2.
| Description | Figure | Moment(s) of inertia | Comment |
|---|---|---|---|
| Thin cylindrical shell with open ends, of radius <math>r<math> and mass <math>m<math> | 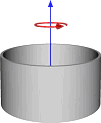 | <math>I = m r^2 \,<math> | — |
| Thick cylinder with open ends, of inner radius <math>r_1<math>, outer radius <math>r_2<math> and mass <math>m<math> | Missing image Moment_of_inertia_thick_cylinder.png Image:moment_of_inertia_thick_cylinder.png | <math>I = \frac{1}{2} m({r_1}^2 + {r_2}^2)<math> | — |
| Solid cylinder of radius <math>r<math>, height <math>h<math> and mass <math>m<math> | 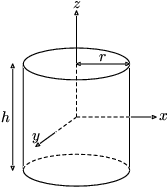 | <math>I_z = \frac{1}{2} mr^2<math> <math>I_x = I_y = \frac{1}{12} m(3r^2+h^2)<math> | — |
| Thin disk of radius <math>r<math> and mass <math>m<math> | Missing image Moment_of_inertia_disc.png Image:moment of inertia disc.png | <math>I_z = \frac{1}{2} mr^2<math> <math>I_x = I_y = \frac{1}{4} m(r^2)<math> | — |
| Solid sphere of radius <math>r<math> and mass <math>m<math> | 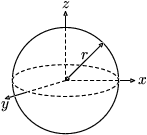 | <math>I = \frac{2}{5} mr^2<math> | — |
| Hollow sphere of radius <math>r<math> and mass <math>m<math> |  | <math>I = \frac{2}{3} mr^2<math> | — |
| Right circular cone with radius <math>r<math>, <math>h<math> and mass <math>m<math> | Missing image Moment_of_inertia_cone.png Image:moment_of_inertia_cone.png |
<math>I_z = (3/10)mr^2 \,\!<math> <math>I_x = I_y = (3/5)m(r^2/4+h^2) \,\!<math> | — |
| Solid rectangular prism of height <math>h<math>, width <math>w<math>, and depth <math>d<math>, and mass <math>m<math> | Missing image Moment_of_inertia_solid_rectangular_prism.png Image:moment_of_inertia_solid_rectangular_prism.png | <math>I_h = \frac{1}{12} m(w^2+d^2)<math> <math>I_w = \frac{1}{12} m(h^2+d^2)<math> <math>I_d = \frac{1}{12} m(h^2+w^2)<math> | For a similarly oriented cube with sides of length <math>s<math> and mass <math>M<math>, <math>I_{CM} = \frac{1}{6} ms^2<math>. |
| Rod of length <math>L<math> and mass <math>m<math> | Missing image Moment_of_inertia_rod_center.png Image:moment_of_inertia_rod_center.png | <math>I_{center} = \frac{1}{12} mL^2<math> | This expression is an approximation, and assumes that the mass of the rod is distributed in the form of an infinitely thin (but rigid) wire. |
| Rod of length <math>L<math> and mass <math>m<math> | 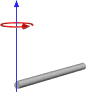 | <math>I_{end} = \frac{1}{3} mL^2<math> | This expression is an approximation, and assumes that the mass of the rod is distributed in the form of an infinitely thin (but rigid) wire. |
Area moments of inertia
Area moments of inertia have units of dimension Length4. Each is with respect to a horizontal axis through the centroid of the given shape, unless otherwise specified.
| Description | Figure | Area Moment(s) of inertia | Comment |
|---|---|---|---|
| a filled circular area of radius <math>r \,<math> | <math>I_0 = \pi r^4/4 \,<math> | ||
| a filled semicircle with radius <math>r \,<math> resting atop the <math>x<math>-axis | <math>I_0 = \pi r^4/8 \,<math> | ||
| a filled quarter circle with radius <math>r \,<math> entirely in the upper-right quadrant of the Cartesian plane | <math>I_0 = \pi r^4/16 \,<math> | ||
| an ellipse whose radius along the <math>x<math>-axis is <math>a \,<math> and whose radius along the <math>y<math>-axis is <math>b \,<math> | <math>I_0 = \pi ab^3/4 \,<math> | ||
| a filled Rectangular area with a base width of <math>b \,<math> and height <math>h \,<math> | <math>I_0 = bh^3/12 \,<math> | ||
| an axis collinear with the base | <math>I = bh^3/3 \,<math> | This is a trivial result from the parallel axis theorem | |
| a filled triangular area with a base width of <math>b \,<math> and height <math>h<math> | <math>I_0 = bh^3/36 \,<math> | ||
| an axis collinear with the base | <math>I = bh^3/12 \,<math> | This is a consequence of the parallel axis theorem and the fact that the distance between these two axes is always <math>h/3 \,<math> |
