Koch curve
|
|
Koch_curve.GIF
| Contents |
Description
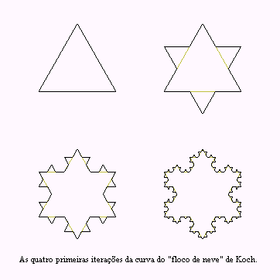
The Koch curve is a mathematical curve, and one of the earliest fractal curves to have been described. It appeared in a 1904 paper entitled "Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire" by the Swedish mathematician Helge von Koch. The better known Koch snowflake (or Koch star) is the same as the curve, except it starts with an equilateral triangle instead of a line segment. Eric Haines has developed the sphereflake fractal, a three-dimensional version of the snowflake.
One can imagine that it was created by starting with a line segment, then recursively altering each line segment as follows:
- divide the line segment into three segments of equal length.
- draw an equilateral triangle that has the middle segment from step one as its base.
- remove the line segment that is the base of the triangle from step 2.
After doing this once the result should be a shape similar to a cross section of a witch's hat.
The Koch curve is in the limit approached as the above steps are followed over and over again.
The Koch curve has infinite length because each time the steps above are performed on each line segment of the figure its length increases by one third. The length at step n will therefore be (4/3)n and the fractal dimension is log4/log3 =~1.26 (bigger than the dimension of a line {1} but smaller than Peano's Space-filling curve {2}).
The Koch curve is continuous, but not differentiable anywhere.
Implementation
Here follows a sample implementation of the Koch curve for a Turtle robot written in a COMAL-like language. It can be tried out online with Web Turtle (http://www.sonic.net/~nbs/webturtle/webturtle.cgi).
; change value of A to change depth of level. 5 is max. LET A 2 ; calculate adjusted side-length LET B 243 REPEAT A LET B B/3 NEXT ; place pointer POINT 150 MOVE 140 POINT 0 ; start GO SIDE RIGHT 120 GO SIDE RIGHT 120 GO SIDE ; finished. END ; main loop # SIDE GO F LEFT 60 GO F RIGHT 120 GO F LEFT 60 GO F RETURN ; forward # F IF A > 1 ; go deeper depending on level LET A A-1 GO SIDE LET A A+1 ELSE ; or just do a single line DRAW B ENDIF RETURN
External link
- More discussion and helpful pictures (http://www.efg2.com/Lab/FractalsAndChaos/vonKochCurve.htm)
See also
es:Copo de nieve de Koch fa:برخال کخ fr:Flocon de Koch ja:コッホ曲線 pt:Curva de Koch ru:Кривая Коха sl:Kochova sneinka sv:Koch-kurvan
