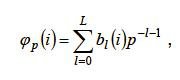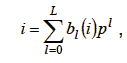Halton sequences
|
|
In statistics, Halton sequences are well-known quasi-random sequences, first introduced in 1960 as an alternative to pseudo-random number sequences. They were designed mainly for use in Monte Carlo simulations of integrals that do not have a closed-form expression in order to achieve variance reduction.
The original Halton sequence is constructed according to a deterministic method that uses a prime number as its base. The one-dimensional Halton sequence based on prime p (≥ 2) fills the 0-1 space by dividing it into p segments, and by systematically filling in the empty spaces, using cycles of length p that place one draw in each segment. A Halton sequence of length N thus consists of an initial cycle of length p-1, in addition to [N-(p-1)]DIV[p] “complete” cycles of length p, and, except in the case where (N+1)MOD(p)=0, also one “incomplete” final cycle of length (N+1)MOD(p).
Formally, φp (i), the i-th element in the Halton sequence based on prime p, is obtained by taking the radical inverse of integer i in base p by reflection through the radical point, such that:
where the values of b0(i), ..., bL(i) are obtained by solving:
Even though standard Halton sequences perform very well in low dimensions, correlation problems have been noted between sequences generated from higher primes. Of course, this indicates serious risk during estimation of high-dimensional integrals (e.g. -- spatial choice modeling, such as location or route). In order to deal with this behavior, various methods have been proposed; one of the most prominent solutions is the scrambled Halton sequence (using predetermined permutations of the coefficients used in the construction of the standard sequence).