HSV color space

The HSV (Hue, Saturation, Value) model, also called HSB (Hue, Saturation, Brightness), defines a color space in terms of three constituent components:

• Hue, the color type (such as red, blue, or yellow):
  • Ranges from 0-360 (but normalized to 0-100% in some applications)
• Saturation, the "vibrancy" of the color:
  • Ranges from 0-100%
  • Also sometimes called the "purity" by analogy to the colorimetric quantities excitation purity and colorimeric purity
  • The lower the saturation of a color, the more "grayness" is present and the more faded the color will appear, thus useful to define desaturation as the qualitative inverse of saturation
• Value, the brightness of the color:
  • Ranges from 0-100%

The HSV model was created in 1978 by Alvy Ray Smith. It is a nonlinear transformation of the RGB color space, and may be used in color progressions. Note that HSV and HSB are the same, but HSL is different.

Contents

1 Visualization of HSV 2 HSV and color perception 3 Transformation from RGB to HSV 4 Transformation from HSV to RGB 5 See also

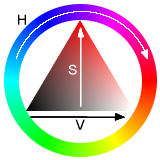
Visualization of HSV

The HSV model is commonly used in computer graphics applications. In various application contexts, a user must choose a color to be applied to a particular graphical element. When used in this way, the HSV color wheel is often used. In it, the hue is represented by a circular region; a separate triangular region may be used to represent saturation and value. Typically, the vertical axis of the triangle indicates saturation, while the horizontal axis corresponds to value. In this way, a color can be chosen by first picking the hue from the circular region, then selecting the desired saturation and value from the triangular region.

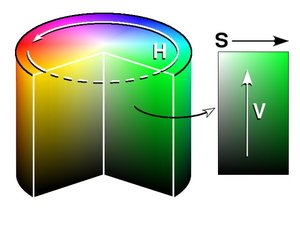
Another visualization method of the HSV model is the cone. In this representation, the hue is depicted as a three-dimensional conical formation of the color wheel. The saturation is represented by the distance from the center of a circular cross-section of the cone, and the value is the distance from the pointed end of the cone. Some representations use a hexagonal cone, or hexcone, instead of a circular cone. This method is well-suited to visualizing the entire HSV color space in a single object; however, due to its three-dimensional nature, it is not well-suited to color selection in two-dimensional computer interfaces.

The HSV color space could also be visualized as a cylindrical object; similar to the cone above, the hue varies along the outer circumference of a cylinder, with saturation again varying with distance from the center of a circular cross-section. Value again varies from top to bottom. Such a representation might be considered the most mathematically accurate model of the HSV color space; however, in practice the number of visually distinct saturation levels and hues decreases as the value approaches black. Additionally, computers typically store RGB values with a limited range of precision; the constraints of precision, coupled with the limitations of human color perception, make the cone visualization more practical in most cases.

HSV and color perception

Artists sometimes prefer to use the HSV color model over alternative models such as RGB or CMYK, because of its similarities to the way humans tend to perceive color. RGB and CMYK are additive and subtractive models, respectively, defining color in terms of the combination of primaries, whereas HSV encapsulates information about a color in terms that are more familiar to humans: What color is it? How vibrant is it? How light or dark is it? The HSL color space is similar and arguably even better than HSV in this respect.

The HSV tristimulus space does not technically support a one-to-one mapping to physical power spectra as measured in radiometry. Thus it is not generally advisable to try to make direct comparisons between HSV coordinates and physical light properties such as wavelength or amplitude. However, if physical intuitions are indispensable, it is possible to translate HSV coordinates into pseudo-physical properties using the psychophysical terminology of colorimetry as follows:

• Hue specifies the dominant wavelength of the color, except in the range between red and indigo (somewhere between 240 and 360 degrees) where the Hue denotes a position along the line of pure purples
• If the hue perception were recreated, actually using a monochromatic, pure spectral color at the dominant wavelength, the desaturation would be roughly analogous to an applied frequency spread around the dominant wavelength or alternatively the amount of equal-power (i.e. white) light added to the pure spectral color.
• The value is roughly analogous to the total power of the spectrum, or the maximum amplitude of the light waveform. However, it should be obvious from the equations below that value is actually closer to the power of the greatest spectral component (the statistical mode, not the cumulative power across the distribution.)

Transformation from RGB to HSV

Given a color defined by (R, G, B) where R, G, and B are between 0.0 and 1.0, with 0.0 being the least amount and 1.0 being the greatest amount of that color, an equivalent (H, S, V) color can be determined by a series of formulas.

Let MAX equal the maximum of the (R, G, B) values, and MIN equal the minimum of those values. The formula can then be written as:

<math>H = \left\{ \begin{matrix} \left( 0 + \frac {G - B} {MAX - MIN} \right) \times 60, & \mbox{if } R = MAX \\ \left( 2 + \frac {B - R} {MAX - MIN} \right) \times 60, & \mbox{if } G = MAX \\ \left( 4 + \frac {R - G} {MAX - MIN} \right) \times 60, & \mbox{if } B = MAX \end{matrix}\right. <math>

<math>S = \frac {MAX - MIN} {MAX}<math>

<math>V = MAX \,<math>

The resulting values are in (H,S,V) form, where H varies from 0.0 to 360.0, indicating the angle in degrees around the color circle where the hue is located. S and V vary from 0.0 to 1.0, with 0.0 being the least amount and 1.0 being the greatest amount of saturation or value, respectively. As an angular coordinate, H can wrap around from 360 back to 0, so any value of H outside of the 0.0 to 360.0 range can be mapped onto that range by dividing H by 360.0 and finding the remainder (also known as modular arithmetic). Thus, -30 is equivalent to 330, and 480 is equivalent to 120, for example.

Note also that the formulas given here reflect some other properties of HSV:

• If MAX = MIN (i.e. S = 0), then H is undefined. This is apparent, considering the diagrams of HSV space above. If S = 0 then the color lies along the central line of grays, so naturally it has no hue, and the angular coordinate is meaningless.
• If MAX = 0 (i.e. if V = 0), then S is undefined. This is best illustrated in the conical diagram above. If V = 0, then the color is pure black, so naturally it has neither hue, nor saturation. Thus the conical diagram collapses to a single point and both the angle and radius coordinates are meaningless at that point.

For those who favor the conical model over the cylinder, a conical space can be achieved by changing the equation for S:

<math>S = MAX - MIN \,<math>.

Transformation from HSV to RGB

Given a color defined by (H, S, V) values, with H, varying between 0.0 and 360.0, indicating the angle, in degrees, around the color circle where the hue is located, and with S and V, varying between 0.0 and 1.0, representing the saturation and value, respectively, a corresponding (R, G, B) color can be determined through a series of formulas.

First, if S is equal to 0.0, then the resulting color is achromatic, or grey. In this special case, R, G, and B are simply equal to V. As above, H is irrelevant in this situation.

When S is non-zero, the following formulas can be used:

<math>H_i = \lfloor { H \over 60 } \rfloor<math>

<math>f = { H \over 60 } - H_i<math>

<math>p = V ( 1 - S ) \,<math>

<math>q = V ( 1 - f S ) \,<math>

<math>t = V ( 1 - ( 1 - f ) S ) \,<math>

<math>\mbox{if } H_i = 0 \rightarrow R = v, G = t, B = p \,<math>

<math>\mbox{if } H_i = 1 \rightarrow R = q, G = v, B = p \,<math>

<math>\mbox{if } H_i = 2 \rightarrow R = p, G = v, B = t \,<math>

<math>\mbox{if } H_i = 3 \rightarrow R = p, G = q, B = v \,<math>

<math>\mbox{if } H_i = 4 \rightarrow R = t, G = p, B = v \,<math>

<math>\mbox{if } H_i = 5 \rightarrow R = v, G = p, B = q \,<math>

See also

• Colorimetry
• Dominant wavelength
• Complementary wavelength
• Saturation
• Color space:
  • RGB color model commonly used for color monitors
  • CMYK color model for color printing
  • HLS color space
  • RYB color model the traditional color model used by artists.
  • YUV for PAL television
  • YIQ for NTSC televisionde:HSV-Farbraum

nl:HSV pl:HSV sv:NMI