Glossary of Riemannian and metric geometry
|
|
This is a glossary of some terms used in Riemannian geometry and metric geometry — it doesn't cover the terminology of differential topology. The following articles may also be useful. These either contain specialised vocabulary or provide more detailed expositions of the definitions given below.
See also:
- Glossary of general topology
- Glossary of differential geometry and topology
- List of differential geometry topics
Unless stated otherwise, letters X, Y, Z below denote metric spaces, M, N denote Riemannian manifolds, |xy| or <math>|xy|_X<math> denotes the distance between points x and y in X. Italic word denotes a self-reference to this glossary.
A caveat: many terms in Riemannian and metric geometry, such as convex function, convex set and others, do not have exactly the same meaning as in general mathematical usage.
| Contents: | top - 0-9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
|---|
A
Alexandrov space a generalization of Riemannian manifolds with upper, lower or integral curvature bounds (the last one works only in dimension 2)
Arc-wise isometry the same as path isometry.
B
Baricenter, see center of mass.
bi-Lipschitz map. A map <math>f:X\to Y<math> is called bi-Lipschitz if there are positive constants c and C such that for any x and y in X
- <math>c|xy|_X\le|f(x)f(y)|_Y\le C|xy|_X<math>
Busemann function given a ray, γ : [0, ∞)→X, the Busemann function is defined by
- <math>B_\gamma(p)=\lim_{t\to\infty}(|\gamma(t)p|-t)<math>
C
Center of mass. A point q∈M is called the center of mass of the points <math>p_1,p_2,..,p_k<math> if it is a point of global minimum of the function
- <math>f(x)=\sum_i |p_ix|^2<math>
Such a point is unique if all distances <math>|p_ip_j|<math> are less than radius of convexity.
Conformally flat a M is conformally flat if it is locally conformally equivalent to a Euclidean space, for example standard sphere is conformally flat.
Conjugate point two points p and q on a geodesic <math>\gamma<math> are called conjugate if there is a Jacobi field on <math>\gamma<math> which has a zero at p and q.
Convex function. A function f on a Riemannian manifold is a convex if for any geodesic <math>\gamma<math> the function <math>f\circ\gamma<math> is convex. A function f is called <math>\lambda<math>-convex if for any geodesic <math>\gamma<math> with natural parameter <math>t<math>, the function <math>f\circ\gamma(t)-\lambda t^2<math> is convex.
Convex A subset K of metric space M is called convex if for any two points in K there is a shortest path connecting them which lies entirely in K, see also totally convex.
D
Diameter of a metric space is the supremum of distances between pairs of points.
Dilation of a map between metric spaces is the infimum of numbers L such that the given map is L-Lipschitz.
E
F
First fundamental form for an embedding or immersion is the pullback of the metric tensor.
G
Geodesic flow is a flow on a tangent bundle TM of a manifold M, generated by a vector field whose trajectories are of the form <math>(\gamma(t),\gamma'(t))<math> where <math>\gamma<math> is a geodesic.
H
Hadamard space is a complete simply connected space with nonpositive curvature.
Horosphere a level set of Busemann function.
I
Injectivity radius at a point p of a Riemannian manifold is the largest radius for which the exponential map at p is a diffeomorphism. Injectivity radius of a Riemannian manifold is the infimum of Injectivity radii at all points.
For complete manifolds, if the injectivity radius at p is a finite, say r, then either there is a geodesic of length 2r which starts and ends at p or there is a point q conjugate to p and on the distance r from p. For closed Riemannian manifold the injectivity radius is either half of minimal length of closed geodesic or minimal distance between conjugate points on a geodesic.
Infranil manifold Given a simply connected nilpotent Lie group N acting on itself by left multiplication and a finite group of automorphisms F of N one can define an action of semidirect product N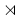 F on N.
A compact factor of N by subgroup of N
F on N.
A compact factor of N by subgroup of N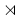 F acting freely on N is called infranil manifold.
Infranil manifolds are factors of nill manifolds by finite group (but wiseversa it is not longer true).
F acting freely on N is called infranil manifold.
Infranil manifolds are factors of nill manifolds by finite group (but wiseversa it is not longer true).
J
Jacobi field is a vector field on a geodesic γ which can be obtained on the following way: Take a smooth one parameter family of geodesics <math>\gamma_\tau<math> with <math>\gamma_0=\gamma<math>, then the Jacobi field
- <math>J(t)=\partial\gamma_\tau(t)/\partial \tau|_{\tau=0}<math>.
K
L
Length metric the same as intrinsic metric.
Levi-Civita connection is a natural way to differentiate vector field on Riemannian manifolds.
Lipschitz convergence the convergence defined by Lipsitz metric.
Lipschitz distance between metric spaces is the infimum of numbers r such that there is a bijective bi-Lipschitz map between these spaces with constants exp(-r), exp(r).
Logarithmic map is a right inverse of Exponential map
M
Metric ball
Minimal surface is a submanifold with (vector of) mean curvature zero.
N
Natural parametrization is the parametrization by length
Net. A sub set S of a metric space X is called <math> \epsilon<math>-net if for any point in X there is a point in S on the distance <math>\le\epsilon<math>. This is distinct from topological nets which generalise limits.
Nil manifolds: the minimal set of manifolds which includes a point, and has the following property: any oriented <math>S^1<math>-bundle over a nil manifold is a nil manifold. It also can be defined as a factor of a connected nilpotent Lie group by a lattice.
Normal bundle....
Nonexpanding map same as short map
P
Polyhedral space a simplicial complex with a metric such that each simplex with induced metric is isometric to a simplex in Euclidean space.
Principal direction
Q
Quasigeodesic. has two meanings here is the most common meaning: A map <math>f:<math>R<math>\to Y<math> is called quasigeodesic if there is a constant C such that
- <math>{1\over C}|xy|-C\le |f(x)f(y)|\le C|xy|+C.<math>
Note that quasigeodesic is not a continuous curve in general.
Quasi-isometry. A map <math>f:X\to Y<math> is called a quasi-isometry if there is a constant C such that f(X) is a C-net in Y and
- <math>{1\over C}|xy|-C\le |f(x)f(y)|\le C|xy|+C.<math>
Note that quasi isometry is not assumed to be continuous, for example any map between compact metric spaces is a quasi isometry.
R
Radius of metric space is the infimum of radii of metric balls which contain the space completely.
Radius of convexity at a point p of a Riemannian manifold is the largest radius of a ball which is a convex subset.
Ray is a one side infinite geodesic which is minimizing on each interval
Riemannian submersion is a map between Riemannian manifolds which is submersion and submetry at the same time.
S
Second fundamental form is a quadratic form on the tangent space of hypersurface, usually denoted by II, an equivalent way to describe shape operator of a hypersurface,
- <math>II(v,w)=\langle S(v),w\rangle<math>
It can be also generalized to arbitrary codimension, then it is a quadratic form with values in the normal space.
Shape operator for a hypersurface M is a linear operator from <math>T_p(M)\to T_p(M)<math>. If n is a unit normal field to M and v is a tangent vector then
- <math>S(v)=\pm \nabla_{v}n<math>
(there is no standard agreement whether to use + or - in the definition).
Short map is a distance non increasing map.
Sol manifold is a factor of a connected solvable Lie group by a lattice.
Submetry a short map f between metric spaces called submetry if for any point x and radius r we have that image of metric r-ball is an r-ball, i.e.
- <math>f(B_r(x))=B_r(f(x))<math>
Systole. k-systole of M, <math>syst_k(M)<math>, is the minimal volume of k-cycle nonhomologous to zero.
T
Totally convex. A subset K of metric space M is called totally convex if for any two points in K any shortest path connecting them lies entirely in K, see also convex.
Totally geodesic submanifold is a submanifold such that all geodesics in the submanifold are also geodesics of the surrounding manifold.
W
Word metric on a group is a metric of the Cayley graph constructed using a set of generators.
