Frieze group

A frieze group is an infinite discrete symmetry group for a pattern on a strip (infinitely wide rectangle). The elements of the group are therefore isometries of the plane, or of a strip. As with Wallpaper groups, Frieze groups are often visualised by this periodic pattern, with the group being those transformations under which the pattern is invariant. There are seven different frieze groups.

A frieze group necessarily contains translations and may contain glide reflections. Other possible group elements are reflections along the long axis of the strip, reflections along the narrow axis of the strip and 180° rotations. Two of the seven frieze groups are singly-generated, four have a pair of generators, and the last of the seven requires three generators.

Each of the frieze groups is a subgroup of this last group, which is the symmetry group of the simplest periodic pattern in the strip (or the plane): a "row of dots" Z × {0} . Any transformation of the plane leaving this pattern invariant can be decomposed into a translation (x,y) → (n+x,y) optionally followed by a reflection in either the horizontal axis (x,y) → (x,-y) or a reflection in the vertical axis (x,y) → (-x,y) or a rotation by 180° (x,y) → (-x,-y). This "largest" frieze group then consists of all such transformations.

The inclusion of the discrete condition is to exclude groups containing all translations, or arbitrarily small translations (e.g. the group of horizontal translations by rational distances) and the inclusion of the infinite condition is to exclude groups that have no translations (e.g. the group consisting of the identity and a vertical reflection only.)

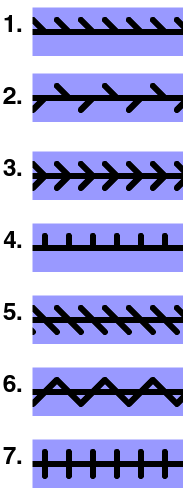
Descriptions of the seven frieze groups

There are seven distinct subgroups (up to scaling) in the discrete frieze group generated by a translation, reflection (along the same axis) and a 180° rotation. Each of these subgroups is the symmetry group of a frieze pattern, and sample patterns are shown in the Fig. 1. The seven different groups can be described as follows:

1. Translations only. This group is singly-generated, with a generator being a translation by the distance over which the pattern is periodic. Consequently the group is isomorphic to Z, the group of integers.
2. Glide-reflections and translations. This group is generated by a single glide reflection, with translations being obtained by combining two glide reflections. Consequently, this group is also isomorphic to Z. (Note that not all glide-reflections are in this group.)
3. Translations, the reflection in the horizontal axis and glide reflections. This group is isomorphic to the direct product Z × C₂, and is generated by a translation and the reflection in the horizontal axis.
4. Translations and reflections across certain vertical lines. The elements in this group correspond to isometries (or equivalently, bijective affine transformations) of the set of integers, and so it is isomorphic to a semidirect product of the integers with C₂, the cyclic group of order 2. The group is generated by a translation and a reflection in a vertical axis.
5. Translations and 180° rotations. Again, the transformations in this group correspond to isometries of the set of integers, and so the group is isomorphic to a semidirect product of Z and C₂. The group is generated by a translation and a 180° rotation.
6. Glide-reflections, translations and rotations. The translations here arise from the glide reflections, so this group is generated by a glide reflection and a rotation. It is isomorphic to a semi-direct product of Z and C₂.
7. Translations, glide reflections, reflections in both axes and 180° rotations. This group is the "largest" frieze group and requires three generators, with one generating set consisting of a translation, the reflection in the horizontal axis and a reflection across a vertical axis. It is isomorphic to a semidirect product of Z × C₂ with C₂.