Finite impulse response
|
|
A finite impulse response (FIR) filter is a type of a digital filter, that is normally implemented through digital electronic computation. The Z-transform of an FIR filter has only zeros and no poles. Digital filters are often characterised by their order which is determined by the number of delay elements , e.g. a second order filter has two delay elements. Alternatively a digital filter may be characterised by the number of taps, which is equal to the order plus one, e.g. a second order filter has three taps.
Z-transform derivation
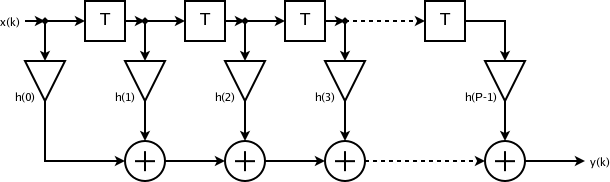
Given a time-invariant input signal <math>x(n)<math> and a Pth-order FIR filter <math>h(n)<math>, the convolution of <math>x<math> with <math>h<math> is defined as follows:
- <math>y(n) = \sum_{k=0}^{P-1} h(k) x(n-k)<math>
The z-transform of <math>h(n)<math>, denoted <math>H(z)<math> is defined as follows:
- <math>H(z) = \sum_{k=0}^{P-1} h(k) z^{-k} = h(0) + h(1) z^{-1} + \cdots + h({P-1})z^{-(P-1)}<math>
The z-transform of <math>y(n)<math> is then <math>Y(z) = H(z) X(z)<math>.
Properties
A FIR filter has a number of useful properties which sometimes make it preferable to an infinite impulse response filter:
- FIR filters are inherently stable
- Require no feedback
- Can have linear phase
An FIR filter has linear phase if and only if its coefficients are symmetric about the center coefficient.