Conic section
|
|
Conic_sections_3.png
Types of conic sections
In mathematics, a conic section (or just conic) is a curved locus of points, formed by intersecting a cone with a plane. The conic sections were named and studied as long ago as 200 BC, when Apollonius of Perga undertook a systematic study of their properties.
| Contents |
Types of conics
Two well-known conics are the circle and the ellipse. These arise when the intersection of cone and plane is a closed curve. The circle is a special case of the ellipse in which the plane is perpendicular to the axis of the cone. If the plane is parallel to a generator line of the cone, the conic is called a parabola. Finally, if the intersection is an open curve and the plane is not parallel to a generator line of the cone, the figure is a hyperbola. (In this case the plane will intersect both halves of the cone, producing two separate curves, though often one is ignored.)
The degenerate cases, where the plane passes through the apex of the cone, resulting in an intersection figure of a point, a straight line or a pair of lines, are often excluded from the list of conic sections.
In the Cartesian coordinate system, the graph of a quadratic equation in two variables is always a conic section, and all conic sections arise in this way. If the equation is of the form
- <math>ax^2 + 2hxy + by^2 +2gx + 2fy + c = 0\;<math>
Conic_sections_2.png
then:
- if h2 = ab, the equation represents a parabola;
- if h2 < ab and a <math> \ne<math> b and/or h<math> \ne<math>0 , the equation represents an ellipse;
- if h2 > ab, the equation represents a hyperbola;
- if h2 < ab and a = b and h = 0, the equation represents a circle;
- if a + b = 0, the equation represents a rectangular hyperbola.
Eccentricity
An alternative definition of conic sections starts with a point F (the focus), a line L (the directrix) not containing F and a positive number e (the eccentricity). The corresponding conic section consists of all points whose distance to F equals e times their distance to L. For 0 < e < 1 we obtain an ellipse, for e = 1 a parabola, and for e > 1 a hyperbola.
For an ellipse and a hyperbola, two focus-directrix combinations can be taken, each giving the same full ellipse or hyperbola. The distance from the center to the directrix is <math>{a}\over{e}<math>, where <math>a<math> is the semi-major axis of the ellipse, or the distance from the center to the tops of the hyperbola. The distance from the center to a focus is <math>ae<math>.
In the case of a circle e = 0 and one imagines the directrix to be infinitely far removed from the center. However, the statement that the circle consists of all points whose distance is e times the distance to L is not useful, because we get zero times infinity.
The eccentricity of a conic section is thus a measure of how far it deviates from being circular.
For a given <math>a<math>, the closer <math>e<math> is to 1, the smaller is the semi-minor axis.
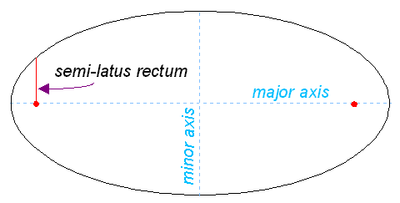
Semi-latus rectum and polar coordinates
The semi-latus rectum of a conic section, usually denoted l, is the distance from the single focus, or one of the two foci, to the conic section itself, measured along a line perpendicular to the major axis. It is related to a and b by the formula <math>al=b^2<math>.
In polar coordinates, a conic section with one focus at the origin and, if any, the other on the positive x-axis, is given by the equation
- <math>r (1 - e \cos \theta) = l. \,<math>
Applications
Conic sections are important in astronomy: the orbits of two massive objects that interact according to Newton's law of universal gravitation are conic sections if their common center of mass is considered to be at rest. If they are bound together, they will both trace out ellipses; if they are moving apart, they will both follow parabolas or hyperbolas. See two-body problem.
In projective geometry, the conic sections in the projective plane are equivalent to each other up to projective transformations.
Dandelin spheres
See Dandelin spheres for a short elementary argument showing that the characterization of these curves as intersections of a plane with a cone is equivalent to the characterization in terms of foci, or of a focus and a directrix.
Derivation
Let there be a cone whose axis is the z-axis. Let its vertex be the origin. The equation for the cone is
- <math> x^2 + y^2 - a^2 z^2 = 0 \qquad \qquad (1) <math>
where
- <math> a = \tan \theta > 0 \;<math>
and <math>\theta <math> is the angle which the generators of the cone make with respect to the axis. Notice that this cone is actually a pair of cones: one cone standing upside down on the vertex of the other cone—or, as mathematicians say, this cone consists of two "nappes."
Let there be a plane with a slope running along the x direction but which is level along the y direction. Its equation is
- <math> z = mx + b \qquad \qquad (2) <math>
where
- <math> m = \tan \phi > 0 \;<math>
and <math>\phi<math> is the angle of the plane with respect to the x-y plane.
We are interested in finding the intersection of the cone and the plane, which means that equations (1) and (2) shall be combined. Both equations can be solved for z and then equate the two values of z. Solving equation (1) for z yields
- <math> z = \sqrt{x^2 + y^2 \over a^2} <math>
therefore
- <math> \sqrt{x^2 + y^2 \over a^2} = m x + b. <math>
Square both sides and expand the squared binomial on the right side,
- <math> {x^2 + y^2 \over a^2} = m^2 x^2 + 2 m b x + b^2. \;<math>
Grouping by variables yields
- <math> x^2 \left( {1 \over a^2} - m^2 \right) + {y^2 \over a^2} - 2 m b x - b^2 = 0. \qquad \qquad (3) <math>
Note that this is the equation of the projection of the conic section on the xy-plane, hence contracted in the x-direction compared with the shape of the conic section itself.
Derivation of the parabola
The parabola is obtained when the slope of the plane is equal to the slope of the generators of the cone. When these two slopes are equal, then the angles <math>\theta <math> and <math>\phi<math> become complementary. This implies that
- <math> \tan \theta = \cot \phi \;<math>
therefore
- <math> m = {1 \over a}. \qquad \qquad (4) <math>
Substituting equation (4) into equation (3) makes the first term in equation (3) vanish, and the remaining equation is
- <math> {y^2 \over a^2} - {2 \over a} b x - b^2 = 0. <math>
Multiply both sides by a2,
- <math> y^2 - 2 a b x - a^2 b^2 = 0 \;<math>
then solve for x,
- <math> x = {1 \over 2 a b} y^2 - {a b \over 2}. \qquad \qquad (5) <math>
Equation (5) describes a parabola whose axis is parallel to the x-axis. Other versions of equation (5) can be obtained by rotating the plane around the z-axis.
Derivation of the ellipse
An ellipse happens when the angles <math>\theta<math> and <math>\phi<math>, when added together, do not measure up to a right angle:
- <math> \theta + \phi < {\pi \over 2} \qquad \qquad \mbox{(ellipse)} <math>
which implies that the tangent of the sum of these two angles is positive.
- <math> \tan (\theta + \phi) > 0. \;<math>
But a trigonometric identity states that
- <math> \tan (\theta + \phi) = {\tan \theta + \tan \phi \over 1 - \tan \theta \tan \phi} <math>
therefore
- <math> \tan (\theta + \phi) = {m + a \over 1 - m a} > 0 \qquad \qquad (6)<math>
but m + a is positive, since the summands are given to be positive, so inequality (6) is positive if the denominator is also positive:
- <math> 1 - m a > 0. \qquad \qquad (7) <math>
From inequality (7) we can deduce
- <math> m a < 1, \;<math>
- <math> m^2 a^2 < 1, \;<math>
- <math> 1 - m^2 a^2 > 0, \;<math>
- <math> {1 \over m^2 a^2} > 1, <math>
- <math> {1 \over m^2 a^2} - 1 > 0, <math>
- <math> {1 \over a^2} - m^2 > 0 \qquad \qquad \mbox{(ellipse)}. <math>
Let us start out again from equation (3),
- <math> x^2 \left( {1 \over a^2} - m^2 \right) + {y^2 \over a^2} - 2 m b x - b^2 = 0, \qquad \qquad (3) <math>
but this time the coefficient of the x2 term does not vanish but is instead positive. Solve for y,
- <math> y = a \sqrt{ b^2 + 2 m b x - x^2 \left( {1 \over a^2} - m^2 \right)}. \qquad \qquad (8) <math>
This would clearly describe an ellipse were it not for the second term under the radical, the 2 m b x: it would be the equation of a circle which has been stretched proportionally along the directions of the x-axis and the y-axis. Equation (8) is an ellipse but it is not obvious, so it will be rearranged further until it is obvious. Complete the square under the radical,
- <math> y = a \sqrt{ b^2 - \left[ x \sqrt{ {1 \over a^2} - m^2} - {b \over \sqrt{ {1 \over a^2 m^2} - 1}} \right]^2 + \left( {b^2 \over {1 \over a^2 m^2} - 1} \right)}. <math>
Group together the b2 terms,
- <math> y = a \sqrt{ b^2 \left( 1 + {1 \over {1 \over a^2 m^2} - 1} \right) - \left[x \sqrt{ {1 \over a^2} - m^2} - {b \over \sqrt{{1 \over a^2 m^2} - 1}} \right]^2 }. <math>
Divide by a then square both sides,
- <math> {y^2 \over a^2} + \left( x \sqrt{{1 \over a^2} - m^2} - {b \over \sqrt{{1 \over a^2 m^2} - 1}} \right)^2 = b^2 \left( 1 + {1 \over {1 \over a^2 m^2} - 1} \right). <math>
The x has a coefficient. It is desired to pull this coefficient out by factoring it out of the second term which is a square,
- <math> {y^2 \over a^2} + \left( {1 \over a^2} - m^2 \right) \left( x - {b \over \sqrt{ \left( {1 \over a^2 m^2} - 1 \right) \left( {1 \over a^2} - m^2 \right)}} \right)^2 = b^2 \left( 1 + { 1 \over {1 \over a^2 m^2} - 1} \right). <math>
Further rearrangements of constants finally leads to
- <math> {y^2 \over 1 - a^2 m^2} + \left( x - {m b \over {1 \over a^2} - m^2} \right)^2 = { a^2 b^2 \over (1 - a^2 m^2)^2}. <math>
The coefficient of the y term is positive (for an ellipse). Renaming of coefficients and constants leads to
- <math> {y^2 \over A} + (x - C)^2 = R^2 \qquad \qquad (9) <math>
which is clearly the equation of an ellipse. That is, equation (9) describes a circle of radius R and center (C,0) which is then stretched vertically by a factor of <math> \sqrt{A} <math>. The second term on the left side (the x term) has no coefficient but is a square, so that it must be positive. The radius is a product of squares, so it must also be positive. The first term on the left side(the y term) has a coefficient which is positive, so the equation describes an ellipse.
Derivation of the hyperbola
The hyperbola happens when the angles <math> \theta <math> and <math> \phi<math> add up to an obtuse angle, which is greater than a right angle. The tangent of an obtuse angle is negative. All the inequalities which were valid for the ellipse become reversed. Therefore
- <math> 1 - a^2 m^2 < 0 \qquad \qquad \mbox{(hyperbola)}. <math>
Otherwise the equation for the hyperbola is the same as equation (9) for the ellipse, except that the coefficient A of the y term is negative. The sign change is enough to convert an ellipse into a hyperbola. This is because the equation of a real ellipse contains an imaginary hyperbola, and the equation of a real hyperbola contains an imaginary ellipse (see imaginary number). The sign change of coefficient A causes real and imaginary values of the function y=f(x) equivalent to equation (9) to swap.
See also
- Focus (geometry), an overview of properties of conic sections related to the foci.
- Quadrics are the higher-dimensional analogs of conics.
- Matrix representation of conic sections.
- Quadratic function.
External links
- Special plane curves: Conic sections (http://xahlee.org/SpecialPlaneCurves_dir/ConicSections_dir/conicSections.html)
- http://mathworld.wolfram.com/Focus.html
- Occurrence of the conics (http://ccins.camosun.bc.ca/~jbritton/jbconics.htm) in nature and elsewhereda:Keglesnit
de:Kegelschnitt es:Sección cónica eo:Koniko fr:Conique id:Irisan kerucut he:חתכי חרוט lt:Kūgio pjūvis nl:Kegelsnede ja:円錐曲線 pl:Krzywa stożkowa pt:Cónicas ru:Коническое сечение sl:Stožnica sv:Kägelsnitt zh:圆锥曲线