Cardioid
|
|
In geometry, the cardioid is an epicycloid which has one and only one cusp. That is, a cardioid is a curve that can be produced as a locus — by tracing the path of a chosen point of a circle which rolls without slipping around another circle which is fixed but which has the same radius as the rolling circle.
The cardioid is also a special type of limašon: it is the limaçon with one cusp. (The cusp is formed when the ratio of a to b in the equation is equal to one.)
The name comes from the heart shape of the curve (Greek kardioeides = kardia:heart + eidos:shape). Compared to the ♥ symbol, though, it doesn't have the sharp point at the bottom.
The cardioid is an inverse transform of a parabola.
The large, central, black figure in a Mandelbrot set is a cardioid. This cardioid is surrounded by a fractal arrangement of circles.
Equations
Since the cardioid is an epicycloid with one cusp, its parametric equations are
- <math> x(\theta) = \cos \theta + {1 \over 2} \cos 2 \theta, \qquad \qquad<math>
- <math> y(\theta) = \sin \theta + {1 \over 2} \sin 2 \theta. \qquad \qquad<math>
The same shape can be defined in polar coordinates by the equation
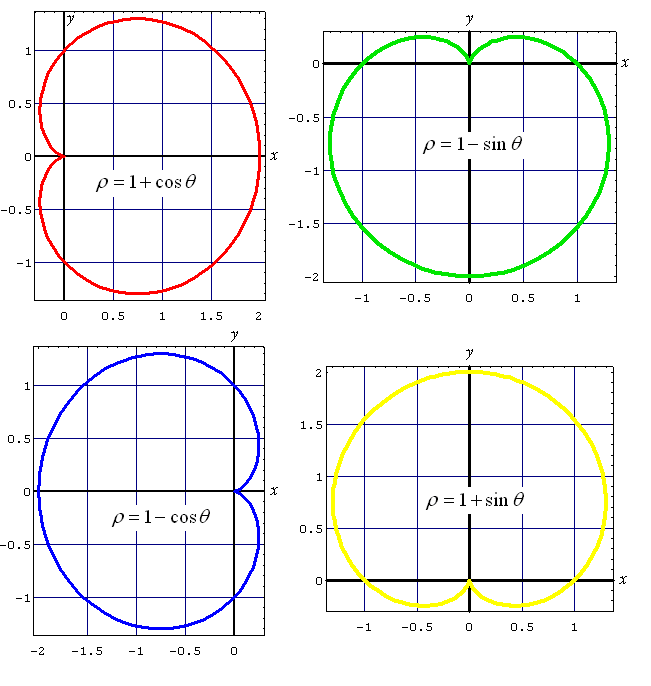
- <math> \rho(\theta) = 1 + \cos \theta. \ <math> (proof)
Graphs
- Four graphs of cardioids oriented in the four cardinal directions, with their respective polar equations.
External link
- Alexander Bogomolny, Hearty Munching on Cardioids (http://www.cut-the-knot.org/ctk/Cardi.shtml) at Cut-the-Knot, (1998)
- Xah Lee, Cardioid (http://www.xahlee.org/SpecialPlaneCurves_dir/Cardioid_dir/cardioid.html) (1998) (This site provides a number of alternative constructions).de:Kardioide