Braid group
|
|
In mathematics, the braid group on n strands, denoted by Bn, is a certain group which has a nice geometrical representation and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group.
Braid groups were introduced explicitly by Emil Artin in 1925, although (as Wilhelm Magnus pointed out in 1974) they were already implicit in Adolf Hurwitz's work on monodromy (1891). In fact, as Magnus says, Hurwitz gave the interpretation of a braid group as the fundamental group of a configuration space, an interpretation that was lost from view until it was rediscovered by Ralph Fox and Lee Neuwirth in 1962!
| Contents |
Intuitive description
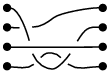
For this introduction, we will take n=4; the generalization to other values of n will be straightforward. Consider two sets of four items lying on a table, with the items in each set being arranged in a vertical line, and such that one set sits next to the other. (In the illustrations below, these are the black dots.) You are given four strands, and you are to connect each item of the first set with an item of the second set so that a one-to-one correspondence results. Such a connection we call a braid. Often some strands will have to pass over or under others, and this is crucial: the following two connections are different braids:
On the other hand, two such connections which can be made to look the same by "pulling the strands" are considered the same braid:
We require that all strands move from left to right; knots like the following are not considered braids:
Now given two braids, we can compose them by drawing the first next to the second, identifying the four items in the middle, and connecting corresponding strands:
Another example:
Missing image
Braid_s1_inv_s3_inv.png
image:braid_s1_inv_s3_inv.png
composed with Missing image
Braid_s1_s3_inv.png
image:braid_s1_s3_inv.png
yields 
The composition of the braids σ and τ is written as στ.
The set of all braids on four strands is denoted by B4. The above composition of braids is indeed a group operation. The neutral element is the braid consisting of four parallel horizontal strands, and the inverse of a braid consists of that braid which "undoes" whatever the first braid did. (Our first two example braids above are inverses of each other.)
Generators and relations
Consider the following three braids:
| Missing image Braid_s1.png image:braid_s1.png |  |  |
σ1 | σ2 | σ3 |
It turns out that every braid can be written as a composition of a number of these braids and their inverses. In other words, these three braids generate the group B4. To see this, take an arbitrary braid and scan it from left to right; whenever you encounter a crossing of strand i and i+1 (counting from the top), write down σi or σi-1, depending on whether strand i moves under or over strand i+1. When you reach the right end, you have written your braid as a product of the σ's and their inverses.
It's clear that
- σ1σ3 = σ3σ1.
The following two relations are not quite as obvious:
- σ1σ2σ1 = σ2σ1σ2
- σ2σ3σ2 = σ3σ2σ3
(Verify these on a piece of paper!)
One can show that all other relations among the braids σ1, σ2 and σ3 already follow from these relations and the group axioms.
So one can abstractly define the group Bn via the following presentation:
- generators σ1,...,σn-1
- relations (known as the braid relations):
- σi σj = σj σi whenever |i -j| ≥ 2 ;
- σi σi+1 σi = σi+1 σi σi+1 for i = 1,..., n-2
Relation to the symmetric group, group actions
Every braid on n strands basically consists of a one-to-one correspondence between two sets of n items, and some topological information about how the strands establish this correspondence. If we forget this topological information, then every braid yields a one-to-one correspondence of n items; these are precisely the elements of the symmetric group Sn. It turns out that this assignment is in fact a surjective group homomorphism Bn → Sn.
The kernel of this group homomorphism is called the pure Braid group on n strands; intuitively, it consists of those braids which connect the i-th item of the left set to the i-th item of the right set, for all i.
The symmetric group Sn has a very similar presentation to the one given above: if you take the braid relations and add the relations
- σi2 = 1 for i=1,...,n-1
then you obtain a presentation for Sn (the σi can then be thought of as transpositions of two neighboring elements).
One frequently encounters a situation where n items are being permuted "up to a twist", and then there is often an underlying group action of a braid group. As a prototypical example, consider an arbitrary group G and the set X of all n-tuples of elements of G whose product is 1. Then Bn operates on X in a natural fashion: given a tuple x = (x1,...,xn) in X, we define σi.x = (x1,...,xi-1,xi+1,xi+1-1xixi+1,xi+2,...,xn). This operation satisfies the braid relations and thus defines a group action of Bn on X.
Some properties
The groups B0 and B1 are trivial; B2 is already infinite and isomorphic to the infinite cyclic group Z. B3 is a quite complicated non-abelian infinite group.
In general, Bn is a subgroup of Bn+1: it can be viewed as consisting of all those braids on n+1 strands in which the bottom strand is horizontal and does not cross nor is crossed by any other strand.
So in particular, Bn is abelian if and only if n ≤ 2.
There is a useful notion of "length" for the elements of the Braid group, given by the group homomorphism w : Bn → Z that maps every σi to 1.
Computational aspects
The word problem for the braid relations is efficiently solvable and there exists a normal form for elements of Bn in terms of the generators σ1,...,σn−1. (In essence, computing the normal form of a braid is the algebraic analogue of "pulling the strands" as illustrated in our second set of images above.) The free GAP computer algebra system can carry out computations in Bn if the elements are given in terms of these generators. There is also a package called CHEVIE for GAP3 with special support for braid groups.
Since there are nevertheless several hard computational problems about braid groups, applications in cryptography have been suggested.
Through cutting, every knot and every link can be represented by a braid (see Alexander's theorem in braid theory). Since braids can be concretely given as words in the σi, this is often the preferred method to enter knots into computer programs.
Formal treatment
To put the above informal discussion of braid groups on firm ground, one needs to use the homotopy concept of algebraic topology. This is outlined in the article on braid theory.
Alternatively, one can eschew topology altogether and define the braid group purely algebraically via the braid relations.