Bertrand's paradox (probability)

There is another, different, Bertrand's paradox related to economics; see Bertrand paradox (economics). This article is about Bertrand's paradox in probability theory.

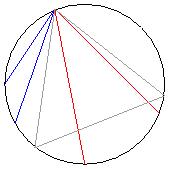
Bertrand's paradox is a problem in probability theory. Consider an equilateral triangle inscribed in a circle. Suppose a chord of the circle is chosen at random. What is the probability that the chord is longer than a side of the triangle?

This problem was originally posed by Joseph Bertrand in his work, Calcul des probabilités (1888). Bertrand gave three arguments, all apparently valid, yet yielding inconsistent results.

1. 

   Random chords, selection method 1; red = longer than triangle side, blue = shorter
   Choose a point on the circle and rotate the triangle so that the point is at one vertex. Choose another point on the circle and draw the chord joining it to the first point. For points on the arc between the endpoints of the side opposite the first point, the chord is longer than a side of the triangle. The length of the arc is one third of the circumference of the circle, therefore the probability a random chord is longer than a side of the inscribed triangle is one third.
   
2. Missing image
   Bertrand2-figure.jpeg

   Random chords, selection method 2
   Choose a radius of the circle and rotate the triangle so a side is perpendicular to the radius. Choose a point on the radius and construct the chord whose midpoint is the chosen point. The chord is longer than a side of the triangle if the chosen point is nearer the center of the circle than the point where the side of the triangle intersects the radius. Since the side of the triangle bisects the radius, it is equally probable that the chosen point is nearer or farther. Therefore the probability a random chord is longer than a side of the inscribed triangle is one half.
   
3. Missing image
   Bertrand3-figure.jpeg

   Random chords, selection method 3
   Choose a point anywhere within the circle and construct a chord with the chosen point as its midpoint. The chord is longer than a side of the inscribed triangle if the chosen point falls within a concentric circle of radius 1/2. The area of the smaller circle is one fourth the area of the larger circle, therefore the probability a random chord is longer than a side of the inscribed triangle is one fourth.
   

Bertrand intended to show that the classical definition of probability is not applicable to a problem with an infinity of possible outcomes. According to the classical definition, the probability of a compound event is the ratio of the number of favorable cases to the total number of cases. Such a definition is inapplicable here, for there are an infinity of chords. Extrapolating the classical definition to ratios of lengths (solutions 1 and 2) or areas (solution 3) seems to yield inconsistent results.

The difficulty hinges on the means by which a chord is chosen "at random". It turns out that once the method of random selection is specified, the problem has a well-defined solution. There is no unique selection method, so there cannot be a unique solution. The three solutions presented by Bertrand correspond to different selection methods, and in the absence of further information there is no reason to prefer one over another.

The selection methods can be visualized as follows. Other than a diameter, a chord is uniquely identified by its midpoint. Each of the three selection methods presented above yields a different distribution of midpoints. Solutions 1 and 2 yield two different nonuniform distributions, while solution 3 yields a uniform distribution. Other distributions can easily be imagined, each of which will yield a different proportion of chords which are longer than a side of the inscribed triangle.

References

• Michael Clarke. Paradoxes from A to Z. London: Routledge, 2002.

External links

• Bertrand's Paradox (http://www.cut-the-knot.org/bertrand.shtml)