Arabic numerals

Template:Table Numeral Systems Arabic numerals (also called Hindu numerals or Indian numerals ) are the most common set of symbols used to represent numbers. They are considered one of the most significant developments in mathematics.

History

What are known in English as "Arabic numerals" were neither invented nor widely used by the Arabs. Instead, they were developed in India by the Hindus around 400 BC. However, because it was Arabs who transmitted this system to the West after the Hindu numerical system found its way to Persia, the numeral system became known as "Arabic". Arabs themselves call the numerals they use "Indian numerals", أرقام هندية, arqam hindiyyah)

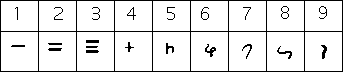
Hindu numerals in the first century AD.

The first inscriptions using 0 in India have been traced to approximately AD 400. Aryabhata's numerical code also represents a full knowledge of the zero symbol. By the time of Bhaskara I (i.e., the seventh century AD) a base 10 numeral system with 9 symbols was widely used in India, and the concept of zero (represented by a dot) was known (see the Vāsavadattā of Subandhu, or the definition by Brahmagupta). It is possible, however, that the invention of the zero sign took place sometime in the first century when the Buddhist philosophy of shunyata (zero-ness) gained ascendancy.

How the numbers came to the Arabs can be read in the work of al-Qifti's "Chronology of the scholars", which was written around the end the 12th century but quoted earlier sources (see [1]):

... a person from India presented himself before the Caliph al-Mansur in the year 776 CE who was well versed in the siddhanta method of calculation related to the movement of the heavenly bodies, and having ways of calculating equations based on the half-chord [essentially the sine] calculated in half-degrees ... Al-Mansur ordered this book to be translated into Arabic, and a work to be written, based on the translation, to give the Arabs a solid base for calculating the movements of the planets ...

This book, which the Indianian scholar presented from, was likely Brahmasphutasiddhanta (The Opening of the Universe) which was written in 628 CE by the Indian mathematician Brahmagupta and had used the Hindi Numerals with the zero sign.

The numeral system came to be known to both the Persian mathematician Al-Khwarizmi, whose book On the Calculation with Hindu Numerals written about 825, and the Arab mathematician Al-Kindi, who wrote four volumes (see [2]) "On the Use of the Indian Numerals" (Ketab fi Isti'mal al-'Adad al-Hindi) about 830, are principally responsible for the diffusion of the Indian system of numeration in the Middle-East and the West . In the tenth century AD, Middle-Eastern mathematicians extended the decimal numeral system to include fractions, as recorded in a treatise by Syrian mathematician Abu'l-Hasan al-Uqlidisi in 952-3.

Fibonacci, an Italian mathematician who had studied in Bejaia (Bougie), Algeria, promoted the Arabic numeral system in Europe with his book Liber Abaci, which was published in 1202. The system did not come into wide use in Europe, however, until the invention of printing (See, for example, the 1482 Ptolemaeus map of the world (http://bell.lib.umn.edu/map/PTO/TOUR/1482u.html) printed by Lienhart Holle in Ulm, and other examples in the Gutenberg Museum in Mainz, Germany.)

It should be noted that in the Arab World—until modern times—the Arabic numeral system was used only by mathematicians. Muslim scientists used the Babylonian numeral system, and merchants used a numeral system similar to the Greek numeral system and the Hebrew numeral system. Therefore, it was not until Fibonacci that the Arabic numeral system was used by a large population.

Description

The numeral set known in English as 'Arabic numerals' is a positional base 10 numeral system with ten distinct symbols representing the 10 numerical digits. Each digit has a value which is multiplied by a power of ten according to its position in the number; the left-most digit of a number has the greatest value.

In a more developed form, the Arabic numeral system also uses a decimal marker (at first a mark over the ones digit but now more usually a decimal point or a decimal comma which separates the ones place from the tenths place), and also a symbol for “these digits repeat ad infinitum” (recur). In modern usage, this latter symbol is usually a vinculum (a horizontal line placed over the repeating digits); the need for it can be removed by representing fractions as simple ratios with a division sign, but this obviates many of Arabic numbers’ more obvious advantages, such as the ability to immediately determine which of two numbers is greater. Historically, however, there has been much variation. In this more developed form, the Arabic numeral system can symbolize any rational number using only 13 symbols (the ten digits, decimal marker, vinculum or division sign, and an optional prepended dash to indicate a negative number).

It is interesting to note that, like in many numbering systems, the numbers 1, 2, and 3 represent simple tally marks. 1 being a single line 2 being two lines (now connected by a diagonal) and 3 being three lines (now connected by two vertical lines). After three numbers tend to become more complex symbols (examples are the Chinese/Japanese numbers and Roman numerals). Theorists believe that this is because it becomes difficult to instantaneously count objects past three.

The Arabic numeral system has used many different sets of symbols. These symbol sets can be divided into two main families—namely the West Arabic numerals, and the East Arabic numerals. East Arabic numerals—which were developed primarily in what is now Iraq—are shown in the table below as Arabic-Indic. East Arabic-Indic is a variety of East Arabic numerals. West Arabic numerals—which were developed in al-Andalus and the Maghreb—are shown in the table, labelled European. (There are two typographic styles for rendering European numerals, known as lining figures and text figures).

Missing image
Arabic_numerals.png
Table of numerals

In Japan, Arabic numerals and the Roman alphabet are both used under the name of rōmaji. So, if a number is written in Arabic numerals, they would say “it is written in rōmaji” (as opposed to Japanese numerals). This translates as ‘Roman characters’, and may sound confusing for those who know about Roman numerals.

Template:Arabic alphabet

External links

Unicode reference charts (http://www.unicode.org/charts/):
- Arabic (http://www.unicode.org/charts/PDF/U0600.pdf) (See codes U+0660-U+0669, U+06F0-U+06F9)
- Devanagari (http://www.unicode.org/charts/PDF/U0900.pdf) (See codes U+0966-U+096F)
- Tamil (http://www.unicode.org/charts/PDF/U0B80.pdf) (See codes U+0BE6-U+0BEF)

History of the Numerals
- The Evolution of Numbers (http://www.laputanlogic.com/articles/2003/06/01-95210802.html)
- Indian numerals (http://www-gap.dcs.st-and.ac.uk/%7Ehistory/HistTopics/Indian_numerals.html):
- Arabic numerals (http://www-gap.dcs.st-and.ac.uk/%7Ehistory/HistTopics/Arabic_numerals.html):
- Hindu-Arabic numerals (http://www.scit.wlv.ac.uk/university/scit/modules/mm2217/han.htm):

Learn Arabic Online - Numerals page (http://st-takla.org/Learn_Languages/01_Learn_Arabic-ta3leem-3araby/Learn-Arabic_01-Alphabet_El-Abgadeya.html) at http://St-Takla.org