Angular frequency
|
|
In SI units, angular frequency is measured in radians per second, with dimensions T−1 since radians are dimensionless.
One revolution is equal to 2π radians, hence
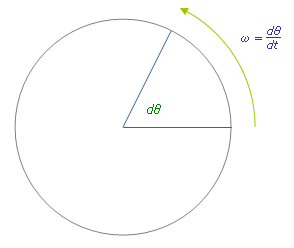
- <math>\omega = {{2 \pi} \over T} = {2 \pi f} = v / r<math>
where
- ω is the angular frequency or angular speed (measured in radians per second),
- T is the period (measured in seconds),
- f is the frequency (measured in hertz),
- v is the tangential velocity of a point about the axis of rotation (measured in metres per second), and
- r is the radius of rotation (measured in metres).
Angular frequency is therefore a simple multiple of ordinary frequency. However, using angular frequency is often preferable in many applications, as it avoids the excessive appearance of <math>\pi<math>. In fact, it is used in many fields of physics involving periodic phenomena, such as quantum mechanics and electrodynamics.
For example:
- <math>
a = - \omega^2 x\; <math>
Using 'ordinary' frequency, this equation would be:
- <math>
a = - 4 \pi^2 f^2 x\;
<math>
See also
de:Kreisfrequenz es:Velocidad angular fr:Vitesse angulaire it:Velocitą angolare ms:Frekuensi angular nl:Hoeksnelheid pl:Pulsacja sl:kotna hitrost vi:Tần số góc