Affine geometry
|
|
In geometry, affine geometry occupies a place intermediate between Euclidean geometry and projective geometry. It is the geometry of affine space, of a given dimension n over a field K. The case where K is the real numbers gives an adequate idea of the content.
| Contents |
Intuitive background
Affine geometry can be explained as the geometry of vectors, not involving any notions of length or angle. Affine space is distinguished from a vector space of the same dimension by 'forgetting' the origin 0. That way of thinking was in older texts sometimes talked about as a theory of free vectors. A contemporary and more abstract way of putting it is mentioned at the end of this page, completing a formal reduction of affine geometry to linear algebra.
Applications and relationships
The notions of affine geometry have applications, for example in differential geometry. Because of the close relation with linear algebra, they are not so often isolated. There do exist several ways, rather than just one, of expressing that relationship.
Affine transformations
Main article: affine transformation.
According to the general scheme of the Erlangen programme, we can say best what affine geometry is by looking at the underlying group of symmetry transformations.
This can be done quickly in terms of a vector space V. The general linear group GL(V) isn't the whole affine group: we must allow also translations by vectors v in V. (Such a translation maps any w in V to w + v.) The affine group is generated by the general linear group and the translations and is in fact their semidirect product V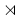 
GL(V). (Here we think of V as a group under its operation of addition, and use the defining representation of GL(V) on V to define the semidirect product.)
Affine theorems
We therefore identify as affine theorems any geometric results that can be stated in terms invariant under the affine group. An example from the plane geometry of triangles is the theorem about the concurrence of the lines joining each vertex to the mid-point of the opposite side (at the centroid or barycentre). The idea of mid-point is an affine invariant. There are other classical examples (theorems of Ceva, Menelaus).
These theorems are notable for having proofs by vector methods. Notice that the logic runs in one direction: if a theorem is an affine theorem, there is no reason why it shouldn't be proved by vectors. It doesn't yet run the other way, that there must be such a proof. That may be desirable from a geometric point of view, rather than finding a heavy-handed proof using analytic geometry. But it's then a question of axiomatic study (so-called synthetic point of view).
Affine invariants can also assist calculations. For example, the lines that divide the area of a triangle into two equal halves form an envelope inside the triangle. The ratio of the area of the envelope to the area of the triangle is affine invariant, and so only needs to be calculated from a simple case such as a unit isosceles right angled triangle to give <math>{3 \over 4} \log_e(2)-{1 \over 2}<math>, i.e. 0.019860... or less than 2%, for all triangles.
What is affine space?
The term affine space is used in projective geometry as the complement of the points (hyperplane) at infinity (see also projective space). There is an implied usage made above: affine space is the space discussed in affine geometry. And there is a third way of defining it, starting from a vector space. Actually the space of translations in an affine space gives back a copy of the underlying vector space anyway. What is required to give a consistent dictionary between all these ways of talking about affine space is the construction of the affine space of a vector space.
Observe that in combinations of vectors v − w the result is unchanged by translation (v moves as much in one direction as − w does in the other) Computationally one must simply restrict discussion to linear combinations of vectors with sum of coefficients equal to zero: these have the same property, and are exactly the sums that can be expressed as combinations of simple differences v − w. This tells us one way to explain the concept of affine space: it's a vector space with the subtraction and scalar multiplication operations. That is one precise way in which to 'forget the origin'.
The abstract definition
This is concise and ultimately more successful (at a price). For any group G there is a notion of principal homogeneous space for G: a set S on which G acts in a way isomorphic to the way it permutes itself by multiplication. An affine space A for a vector space V is just such a principal homogeneous space; one then has to recover scalar multiplication on A as a well-defined concept.de:Affine Geometrie ru:Аффинная геометрия