Adiabatic process
|
|
This article covers adiabatic processes in thermodynamics. For adiabatic processes in quantum mechanics, see adiabatic process (quantum mechanics).
In thermodynamics, an adiabatic process is a process in which no heat is gained or lost in the working fluid. For example, there are no chemical processes taking place in the fluid and there is no heat transfer from the environment. The term "adiabatic" describes things that are impermeable to heat transfer; for example, an adiabatic boundary is a boundary that is impermeable to heat transfer. An insulated wall approximates an adiabatic boundary. Another example is the adiabatic flame temperature, which is the temperature that would be achieved by a flame in the absence of heat loss to the surroundings. An adiabatic process which is also reversible is called an isentropic process.
The opposite extreme, in which the maximum heat transfer with its surroundings occurs, causing the temperature to remain constant, is known as an isothermal process.
Adiabatic heating and cooling are processes that commonly occur due to a change in the pressure of a gas. This can be quantified using the ideal gas law.
There are three rates of adiabatic cooling for air.
- The ambient atmosphere lapse rate, which is the rate that air cools as one goes up in altitude.
- The dry adiabatic lapse rate, -10°C per 1000m rise.
- The wet adiabatic lapse rate, about -6° per 1000m rise.
The first rate is used to describe the temperature of the surrounding air that the rising air is passing through, and the second and third rates are in reference to a parcel of air that is rising through the atmosphere. The dry adiabatic lapse rate applies to air which is below its dew point, ie which is not saturated by water vapor, whereas the wet adiabatic lapse rate applies to air which has reached its dew point. Adiabatic cooling is a common cause of cloud formation.
Adiabatic cooling does not have to involve a fluid. One technique used to reach very low temperatures (thousandths and even millionths of a degree above absolute zero) is adiabatic demagnetisation, where the change in magnetic field on a magnetic material is used to provide adiabatic cooling.
| Contents |
Formula
The mathematical equation for fluid undegoing an adiabatic process is
- <math> P V^{\gamma} = \operatorname{constant} \qquad <math>
where P is pressure, V is volume, and
- <math> \gamma = {C_{P} \over C_{V}}, <math>
<math> C_{P} <math> being the molar specific heat for constant pressure and <math> C_{V} <math> being the molar specific heat for constant volume. For a monatomic ideal gas, <math> \gamma = 5/3 <math>, and for a diatomic gas (such as nitrogen and oxygen, the main components of air) <math> \gamma = 1.4 <math>. Note that the above formula is only applicable to classical gases and not Bose-Einstein or Fermi gases.
Derivation of Formula
The definition of an adiabatic process is that heat transfer to the system is zero, <math> Q=0 <math>. Then, according to the first law of thermodynamics,
- <math> \Delta E + W = 0 \qquad \qquad \qquad (1) <math>
where E is the internal energy of the system and W is work done by the system. Any work (W) done must be done at the expense of internal energy E, since no heat Q is being supplied from the surroundings. Pressure-volume work W done by the system is defined as
- <math> W = P \Delta V. \qquad \qquad \qquad (2)<math>
However, P does not remain constant during an adiabatic process but instead changes along with V.
It is desired to know how the values of <math> \Delta P <math> and <math> \Delta V <math> relate to each other as the adiabatic process proceeds. It will now be assumed that the system is a monatomic gas, so that
- <math> C_{V} = {3 \over 2} R <math>
where R is the universal gas constant.
Given <math> \Delta P <math> and <math> \Delta V <math> then <math> W = P \Delta V <math> and
- <math> \Delta E = {3 \over 2} n R \Delta T
= {3 \over 2} \Delta (P V)
= {3 \over 2} (P \Delta V + V \Delta P). \qquad (3)<math>
Now plug equations (2) and (3) into equation (1) to obtain
- <math> -P \Delta V = {3 \over 2} P \Delta V + {3 \over 2} V \Delta P <math>
simplify,
- <math> - {5 \over 2} P \Delta V = {3 \over 2} V \Delta P <math>
divide both sides by PV,
- <math> -5 {\Delta V \over V} = 3 {\Delta P \over P}. <math>
From the differential calculus it is then known that
- <math> -5 \Delta (\operatorname{ln} V) = 3 \Delta (\operatorname{ln} P) <math>
which can be expressed as
- <math> {\operatorname{ln} P - \operatorname{ln} P_0 \over \operatorname{ln} V - \operatorname{ln} V_0 } = -{5 \over 3} <math>
for certain constants <math> P_0 <math> and <math> V_0 <math> of the initial state. Then
- <math> {\operatorname{ln} (P/P_0) \over \operatorname{ln} (V/V_0)} = -{5 \over 3}, <math>
- <math>
\operatorname{ln} \left( {P \over P_0} \right) = \operatorname{ln} \left( {V \over V_0} \right)^{-5/3} <math>
Exponentiate both sides,
- <math> \left( {P \over P_0} \right)
= \left( {V \over V_0} \right)^{-5/3} <math> eliminate the minus sign,
- <math> \left( {P \over P_0} \right)
= \left( {V_0 \over V} \right)^{5/3} <math> therefore
- <math> \left( {P \over P_0} \right) \left( {V \over V_0} \right)^{5/3} = 1
<math> and
- <math> P V^{5/3} = P_0 V_0^{5/3} = \operatorname{constant}. <math>
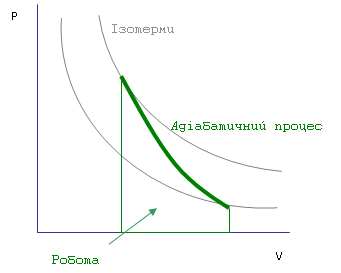
Graphing Adiabats
Properties of adiabats on a P-V diagram are:
(1) every adiabat asymptotically approaches both the V axis and the P axis (just like isotherms).
(2) each adiabat intersects each isotherm exactly once.
(3) an adiabat looks similar to an isotherm, except that during an expansion, an adiabat loses more pressure than an isotherm, so it has a steeper inclination (more vertical).
(4) if isotherms are concave towards the "north-east" direction (45 °), then adiabats are concave towards the "east north-east" (31 °).
(5) If adiabats and isotherms are graphed severally at regular changes of entropy and temperature, respectively (like altitude on a contour map), then as the eye moves outwards away from the axes (towards the north-east), it sees the density of isotherms stay constant, but it sees the density of adiabats drop. The exception is very near absolute zero, where the density of adiabats drops sharply and they become rare (see Nernst's theorem).
The following diagram is a P-V diagram with a superposition of adiabats and isotherms:
The isotherms are the red curves and the adiabats are the black curves. The adiabats are isentropic. Volume is the abscissa and pressure is the ordinate.
See also
- isothermal process
- thermodynamic entropy
- isochoric process
- isobaric process
- cyclic process
- first law of thermodynamics
da:Adiabatisk de:Adiabatische Zustandsänderung es:Proceso adiabático ja:æç±éç¨ nl:adiabatisch pl:Przemiana adiabatyczna sl:adiabatna sprememba sv:Abiabatisk process

