Digital waveguide synthesis
|
|
Digital waveguide synthesis is the synthesis of audio using a digital waveguide. Digital waveguides are efficient computational models for physical media through which acoustic waves propagate. For this reason, digital waveguides constitute a major part of most modern physical modelling synthesizers.
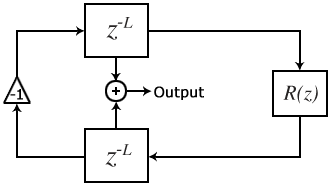
A lossless digital waveguide realizes the discrete form of d'Alembert's solution of the one dimensional wave equation as the superposition of a right-going wave and a left-going wave,
- <math>y(m,n) = y^{+}(m-n) + y^{-}(m+n)<math>
where <math>y^{+}<math> is the right-going wave and <math>y^{-}<math> is the left-going wave. It can be seen from this representation that sampling the function <math>y<math> at a given point <math>m<math> and time <math>n<math> merely involves summing two delayed copies of its travelling waves.
Digital waveguide models are therefore comprised of delay lines to represent the geometry of the waveguide, digital filters to represent the frequency-dependent losses and dispersion in the medium, and often include non-linear elements. Losses incurred throughout the medium are generally consolidated so that they can be calculated once at the termination of a delay line, rather than many times throughout.
Although waveguides such as a acoustic tubes may be thought of as three-dimensional, because their lengths are often much greater than their cross-sectional area, it is reasonable and computationally efficient to model them as one dimensional waveguides. Membranes, as used in drums, may be modelled using two-dimensional waveguide meshes, and reverberation in three dimensional spaces may be modelled using three-dimensional meshes.
Digital waveguide synthesis was developed by Julius O. Smith III and represents an extension of the Karplus-Strong algorithm. Stanford University owns the patent for digital waveguide synthesis and signed an agreement in 1989 to develop the technology with Yamaha.
An extension to DWG synthesis of strings made by Smith is commuted synthesis, wherein the excitation to the digital waveguide contains both string excitation and the body response of the instrument. This is possible because the digital waveguide is linear and makes it unnecessary to model the instrument body's resonances after synthesizing the string output, greatly reducing the number of computations required for a convincing resynthesis.
See also
- Frequency modulation synthesis
- Subtractive synthesis
- Additive synthesis
- Wavetable synthesis
- Physical modelling synthesis
External links
- Julius O. Smith III's A Basic Introduction to Digital Waveguide Synthesis (http://ccrma-www.stanford.edu/~jos/swgt/swgt.html)