Integral
|
|
- This article deals with the concept of an integral in calculus. For other meanings of "integral" see integration and integral (disambiguation).
In calculus, the integral of a function is a generalization of area, mass, volume, sum, and total. The process of finding integrals is integration, in its mathematical meaning. Unlike the closely-related process of differentiation, there are several possible definitions of integration, with different technical underpinnings. They are, however, compatible. Any two different ways of integrating a function will give the same result if they are both defined.
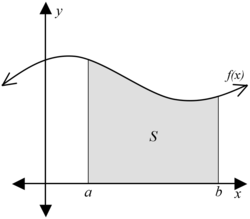
Intuitively, the integral of a continuous, positive real-valued function f of one real variable x between a left endpoint a and a right endpoint b represents the area bounded by the lines x=a, x=b, the x-axis, and the curve defined by the graph of f. More formally, if we let
- <math> S= \{(x,y) \in \mathbb{R}^2:a \leq x \leq b ,0 \leq y \leq f(x)\}, <math>
then the integral of f between a and b is the measure of S.
Leibniz introduced the standard long s notation for the integral. The integral of the previous paragraph would be written <math>\int_a^b f(x)\,dx<math>. The ∫ sign represents integration, a and b are the endpoints of the interval, f(x) is the function we are integrating, and dx is a notation for the variable of integration. Historically, dx represented an infinitesimal quantity, and the long s stood for "sum". However, modern theories of integration are built from different foundations, and the traditional symbols have become no more than notation.
As an example, if f is the constant function f(x)=3, then the integral of f between 0 and 10 is the area of the rectangle bounded by the lines x=0, x=10, y=0, and y=3. The area is the width of the rectangle times its height, so the value of the integral is 30.
Integrals can be taken over regions other than intervals. In general, the integral over a set E of a function f is written ∫Ef(x)dx. Here x need not be a real number, but, for instance, a vector in R3. Fubini's theorem shows that such integrals can be rewritten as an iterated integral. In other words, the integral can be calculated by integrating one coordinate at a time.
If a function has an integral, it is said to be integrable. The function for which the integral is calculated is called the integrand. Integrals are sometimes called definite integrals to emphasize that they result in a number, not another function. This is to distinguish them from indefinite integrals, which are another name for an antiderivative. If the domain of the function to be integrated is the real numbers, and if the region of integration is an interval, then the greatest lower bound of the interval is called the lower limit of integration, and the least upper bound is called the upper limit of integration.
| Contents |
Computing integrals
The most basic technique for computing integrals of one real variable is based on the Fundamental Theorem of Calculus. It proceeds like this:
- Choose a function f(x) and an interval [a,b].
- Find an antiderivative of f, that is, a function F such that F' =f.
- By the Fundamental Theorem of Calculus, <math>\int_a^b f(x)\,dx = F(b)-F(a)<math>.
- Therefore the value of the integral is F(b)-F(a).
Note that the integral is not actually the antiderivative (it is a number), but the fundamental theorem allows us to use antiderivatives to evaluate integrals.
The difficult step is finding an antiderivative of f. It is rarely possible to glance at a function and write down its antiderivative. More often, it is necessary to use one of the many techniques that have been developed to evaluate integrals. Most of these techniques rewrite one integral as a different one which is hopefully more tractable. Techniques include:
- Integration by substitution.
- Integration by parts.
- Integration by trigonometric substitution.
- Integration by partial fractions.
Even if these techniques fail, it may still be possible to evaluate a given integral. The next most common technique is residue calculus. There are also many less common ways of calculating definite integrals; for instance, Parseval's identity can be used to transform an integral over a rectangular region into an infinite sum. Occasionally, an integral can be evaluated by a trick; for an example of this, see Gaussian integral.
Computations of volumes of solids of revolution can usually be done with disk integration or shell integration.
Specific results which have been worked out by various techniques are collected in the list of integrals.
Approximation of definite integrals
Definite integrals may be approximated using several methods of numerical integration. One popular method, called the rectangle method, relies on dividing the region under the function into a series of rectangles and finding the sum. Other well-known methods are the trapezoidal rule and Simpson's rule.
Some integrals cannot be found exactly, and others are so complex that finding the exact answer would be extremely time-consuming or computationally-intensive. Approximation, however, is a process which relies only on variable substitution, multiplication, addition, and division. It can be done easily and quickly by modern graphing calculators and computers. Many real-world applications of calculus rely on calculating integrals approximately because of the complexity of formulas and since an exact answer is unnecessary.
Integrals and computerized algebra systems
Many professionals, educators, and students now use computerized algebra systems to make difficult (or simply tedious) algebra and calculus problems easier. The design of such a computer algebra system is nontrivial as systematic methods of antidifferentiation are difficult to formulate.
One difficulty is that it is not always possible to find "explicit formulae" for antiderivatives. For instance, there is a (nontrivial) proof that there is no nice function (e.g., involving sin, cos, exp, polynomials, roots and so on) whose derivative is exp(−x2). As such, computerized algebra systems have no hope of being able to find an antiderivative for this particular function. Unfortunately, functions that have nice antiderivatives are the exception. If one writes a large random expression involving exponentials and polynomials, the odds are almost nil that it will have an antiderivative. (This statement can be made formal, but it is difficult to do so.)
One of the difficulties is to decide what set of functions to use as building blocks for antiderivatives. Usually, we need a set of antiderivatives closed under, say, multiplication and composition. This set of antiderivatives should also include polynomials, perhaps quotients, exponentials, logarithms, sines and cosines. The Risch-Norman algorithm is able to compute any integral of such a shape; that is, if the antiderivative involves polynomials, sines, cosines, etc..., the Risch-Norman algorithm will be able to compute it. Extended versions of this algorithm are implemented in Mathematica and the Maple computer algebra system.
Some special integrands occur often enough to warrant special study. In particular, it may be useful to have, in the set of antiderivatives, the special functions of physics (like the Legendre functions, the hypergeometric function, the Gamma function and so on). Extending the Risch-Norman algorithm so that it includes these functions is possible but challenging.
Most humans are not able to integrate such general formulae, so in a sense computers are more skilled at integrating highly complicated formulae. On the other hand, very complex formulae are unlikely to have closed-form antiderivatives, so this advantage is dubious.
Improper integrals
Not all integrals can be evaluated using a single limit process. An integral which can only be evaluated by considering it as the limit of integrals on successively larger and larger intervals is called an improper integral. Improper integrals usually turn up when the range of the function to be integrated is infinite or, in the case of the Riemann integral, when the domain of the function is infinite. One common example of an improper integral is the Cauchy principal value.
Definitions of the integral
The most important integrals are the Riemann integral and the Lebesgue integral. The Riemann integral was created by Bernhard Riemann in 1854 and was the first rigorous definition of the integral. The Lebesgue integral was created by Henri Lebesgue to integrate a wider class of functions and to prove very strong theorems about interchanging limits and integrals.
Although the Riemann and Lebesgue integrals are the most important ones, a number of others exist, including but not limited to:
- The Daniell integral.
- The Darboux integral, a variation of the Riemann integral.
- The Denjoy integral (also known as the Henstock-Kurzweil integral), an extension of both the Riemann and Lebesgue integrals.
- The Haar integral.
- The Henstock-Kurzweil integral, an extension of both the Riemann and Lebesgue integrals (also called HK-integral).
- The Henstock-Kurzweil-Stieltjes integral (also called HK-Stieltjes integral).
- The Lebesgue-Stieltjes integral (also called Lebesgue-Radon integral).
- The Perron integral, which is equivalent to the restricted Denjoy integral.
- The Riemann-Stieltjes integral, an extension of the Riemann integral.
See also
External links
- Riemann Sums - Function Integration (a Java simulation) (http://www.cut-the-knot.org/Curriculum/Calculus/RiemannSums.shtml)
- Function, Derivative and Integral (a Java simulation) (http://www.cut-the-knot.org/Curriculum/Calculus/CubicSpline.shtml)
- The Integrator (http://integrals.wolfram.com/) by Wolfram Research
- Function Calculator (http://wims.unice.fr/wims/wims.cgi?module=tool/analysis/function.en) from WIMS
cs:Integrál de:Integralrechnung eo:Integralo fr:Intégrale is:Heildun it:Integrale he:אינטגרל hu:IntegrálszámÃtás nl:Integraalrekening no:Integral (matematikk) ja:積分 lt:Integralas pl:Całka pt:Integral ro:Integrală sr:Интеграл sv:Integral vi:Tích phân zh:积分