Derivative
|
|
In mathematics, the derivative of a function is one of the two central concepts of calculus. (The other one is the antiderivative, the inverse of the derivative.)
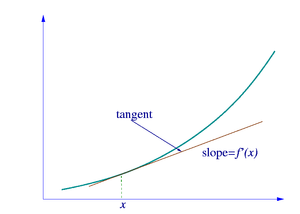
The derivative of a function at a point measures the rate at which the function's value changes as the function's argument changes. That is, a derivative provides a mathematical formulation of the notion of rate of change. As it turns out, the derivative is an extremely versatile concept which can be viewed in many different ways. For example, referring to the two-dimensional graph of f, the derivative can also be regarded as the slope of the tangent to the graph at the point x. The slope of this tangent can be approximated by a secant. Given this geometrical interpretation, it is not surprising that derivatives can be used to determine many geometrical properties of graphs of functions, such as concavity or convexity.
It should be noted that not all functions have derivatives. For example, functions do not have derivatives at points where they have either a vertical tangent or a discontinuity. However, functions may fail to have derivatives even if they are continuous and have no vertical tangents.
| Contents |
Differentiation and differentiability
In somewhat dated language, differentiation expresses the rate at which one quantity y changes as a result of a change in another quantity x on which it has a functional relationship. Using the symbol Δ to refer to change in a quantity, this rate is defined as a limit of difference quotients
- <math> \frac{\Delta y}{\Delta x} <math>
as Δx approaches 0. In Leibniz's notation, the derivative of y with respect to x is written
- <math> \frac{dy}{dx} <math>
suggesting the ratio of two infinitesimal quantities. The above expression is pronounced in various ways such as "dy by dx" or "dy over dx". The form "dy dx" is also used conversationally, although it may be confused with the notation for element of area.
In contemporary mathematical language, one dispenses with referring to dependent quantities and simply states that differentiation is a mathematical operation on functions. The precise definition of this operation (which also dispenses with referring to infinitesimal quantities) is given as:
- <math>\lim_{h \to 0}\frac{f(x+h) - f(x)}{h}.<math>
This definition is discussed in more detail below. If f is a function, the derivative of the function f at the value x is written in several ways:
- <math> f'(x) \quad<math>
pronounced "f prime of x"
- <math> \frac{d}{dx} f (x) <math>
pronounced "d by d x of f of x" or "d d x of f of x".
- <math> \frac{df}{dx} <math>
pronounced "d f by d x" or "d f d x"
- <math> D_x f \quad <math>
pronounced "d sub x of f"
- <math>\dot{x}<math>
pronounced "dot x".
A function is differentiable at a point x if its derivative exists at that point; a function is differentiable on an interval if it is differentiable at every x within the interval. If a function is not continuous at x, then there is no tangent line and the function is therefore not differentiable at x; however, even if a function is continuous at x, it may not be differentiable there. In other words, differentiability implies continuity, but not vice versa.
The derivative of a differentiable function can itself be differentiable. The derivative of a derivative is called a second derivative. Similarly, the derivative of a second derivative is a third derivative, and so on.
Newton's difference quotient
The derivative of a function f at x is geometrically the slope of the tangent line to the graph of f at x. Without the concept which we are about to define, it is impossible to directly find the slope of the tangent line to a given function, because we only know one point on the tangent line, namely (x, f(x)). Instead, we will approximate the tangent line with multiple secant lines that have progressively shorter distances between the two intersecting points. When we take the limit of the slopes of the nearby secant lines in this progression, we will get the slope of the tangent line. The derivative is then defined by taking the limit of the slope of secant lines as they approach the tangent line.
Secant-calculus.png
To find the slopes of the nearby secant lines, choose a small number h. h represents a small change in x, and it can be either positive or negative. The slope of the line through the points (x,f(x)) and (x+h,f(x+h)) is
- <math>{f(x+h)-f(x)\over h}.<math>
This expression is Newton's difference quotient. The derivative of f at x is the limit of the value of the difference quotient as the secant lines get closer and closer to being a tangent line:
- <math>f'(x)=\lim_{h\to 0}{f(x+h)-f(x)\over h}.<math>
Lim-secant.png
If the derivative of f exists at every point x in the domain, we can define the derivative of f to be the function whose value at a point x is the derivative of f at x.
Since immediately substituting 0 for h results in division by zero, calculating the derivative directly can be unintuitive. One technique is to simplify the numerator so that the h in the denominator can be cancelled. This happens easily for polynomials; see calculus with polynomials. For almost all functions however, the result is a mess. Fortunately, many guidelines exist.
Notations for differentiation
The simplest notation for differentiation that is in current use is due to Lagrange and uses the prime, ′. To take derivatives of f(x) at the point a, we write:
- f ′(a) for the first derivative,
- f ″(a) for the second derivative,
- f ″′(a) for the third derivative and then
- f(n)(a) for the nth derivative (n > 3).
For the function whose value at each x is the derivative of f(x), we write f ′(x). Similarly, for the second derivative of f we write f ″(x), and so on.
The other common notation for differentiation is due to Leibniz. For the function whose value at x is the derivative of f at x, we write:
- <math>\frac{d\left(f(x)\right)}{dx}.<math>
We can write the derivative of f at the point a in two different ways:
- <math>\frac{d\left(f(x)\right)}{dx}\left.{\!\!\frac{}{}}\right|_{x=a} = \left(\frac{d\left(f(x)\right)}{dx}\right)(a).<math>
If the output of f(x) is another variable, for example, if y=f(x), we can write the derivative as:
- <math>\frac{dy}{dx}.<math>
Higher derivatives are expressed as
- <math>\frac{d^n\left(f(x)\right)}{dx^n}<math> or <math>\frac{d^ny}{dx^n}<math>
for the n-th derivative of f(x) or y respectively. Historically, this came from the fact that, for example, the 3rd derivative is:
- <math>\frac{d \left(\frac{d \left( \frac{d \left(f(x)\right)} {dx}\right)} {dx}\right)} {dx}<math>
which we can loosely write as:
- <math>\left(\frac{d}{dx}\right)^3 \left(f(x)\right) =
\frac{d^3}{\left(dx\right)^3} \left(f(x)\right).<math>
Dropping brackets gives the notation above.
Leibniz's notation is versatile in that it allows one to specify the variable for differentiation (in the denominator). This is especially relevant for partial differentiation. It also makes the chain rule easy to remember, because the "d" terms appear symbolically to cancel:
- <math>\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}.<math>
(In the popular formulation of calculus in terms of limits, the "d" terms cannot literally cancel, because on their own they are undefined; they are only defined when used together to express a derivative. In nonstandard analysis, however, they can be viewed as infinitesimal numbers that cancel.)
Newton's notation for differentiation was to place a dot over the function name:
- <math>\dot{x} = \frac{dx}{dt} = x'(t)<math>
- <math>\ddot{x} = x''(t)<math>
and so on.
Newton's notation is mainly used in mechanics, normally for time derivatives such as velocity and acceleration, and in ODE theory. It is usually only used for first and second derivatives.
Critical points
Points on the graph of a function where the derivative is undefined or equals zero are called critical points or sometimes stationary points (in the case where the derivative equals zero). If the second derivative is positive at a critical point, that point is a local minimum; if negative, it is a local maximum; if zero, it may or may not be a local minimum or local maximum. Taking derivatives and solving for critical points is often a simple way to find local minima or maxima, which can be useful in optimization. In fact, local minima and maxima can only occur at critical points. This is related to the extreme value theorem.
Notable derivatives
- For general cases:
- <math>\frac{\,d}{\,dx}\,C=0<math>
- <math>\frac{\,d}{\,dx}x^n = nx^{n-1}<math>.
- For logarithmic functions:
- The derivative of ln x is <math>\frac{1}{x}<math>.
- The derivative of <math>\log_b x = \frac{1}{x\ln b}<math>
- For Exponential functions:
- <math>\frac{\,d}{\,dx}<math>ex<math> = e^x<math>
- <math>\frac{d}{\,dx}a^x = a^x \ln a<math>
- For trigonometric functions
- <math>\frac{\,d}{\,dx}\sin x=\cos x<math>.
- <math>\frac{\,d}{\,dx}\cos x = -\sin x<math>.
- <math>\frac{\,d}{\,dx}\tan x = \sec^2 x<math>.
- <math>\frac{\,d}{\,dx}\csc x = -\csc x\cot x<math>.
- <math>\frac{\,d}{\,dx}\sec x = \sec x \tan x<math>.
- <math>\frac{\,d}{\,dx}\cot x = -\csc^2 x<math>.
Physics
Arguably the most important application of calculus to physics is the concept of the "time derivative" — the rate of change over time — which is required for the precise definition of several important concepts. In particular, the time derivatives of an object's position are significant in Newtonian physics:
- Velocity (instantaneous velocity; the concept of average velocity predates calculus) is the derivative (with respect to time) of an object's position.
- Acceleration is the derivative (with respect to time) of an object's velocity.
- Jerk is the derivative (with respect to time) of an object's acceleration.
For example, if an object's position <math>p(t) = -16t^2 + 16t + 32<math>; then, the object's velocity is <math>\dot p(t) = p'(t) = -32t + 16<math>; the object's acceleration is <math>\ddot p(t) = p''(t) = -32<math>; and the object's jerk is <math>p'''(t) = 0.<math>
If the velocity of a car is given, as a function of time; then, the derivative of said function with respect to time describes the acceleration of said car, as a function of time.
Algebraic manipulation
Messy limit calculations can be avoided, in certain cases, because of differentiation rules which allow one to find derivatives via algebraic manipulation; rather than by direct application of Newton's difference quotient. One should not infer that the definition of derivatives, in terms of limits, is unnecessary. Rather, that definition is the means of proving the following "powerful differentiation rules"; these rules are derived from the difference quotient.
- Constant rule: The derivative of any constant is zero.
- Constant multiple rule: If c is some real number; then, the derivative of <math>cf(x)<math> equals c multiplied by the derivative of f(x) (a consequence of linearity below)
- Linearity: (af + bg)' = af ' + bg' for all functions f and g and all real numbers a and b.
- General power rule (Polynomial rule): If <math>f(x) = x^r<math>, for some real number r; <math>f'(x) = rx^{r-1}.<math>
- Product rule: (fg)' = f 'g + fg' for all functions f and g.
- Quotient rule: <math>(f/g)' = (f 'g - fg')/(g^2)<math> unless g is zero.
- Chain rule: If f(x) = h(g(x)), then f '(x) = h'[g(x)] * g'(x).
- Inverse functions and differentiation: If <math>y = f(x)<math>, <math>x = f^{-1}(y)<math>, and f(x) and its inverse are differentiable, with <math>dy/dx<math> non-zero, then <math>dx/dy = 1/(dy/dx).<math>
- Derivative of one variable with respect to another when both are functions of a third variable: Let <math>x = f(t)<math> and <math>y = g(t)<math>. Now <math>d y/d x = (d y/d t)/(d x/d t).<math>
- Implicit differentiation: If <math>f(x,y) = 0<math> is an implicit function, we have: dy/dx = - (∂f / ∂x) / (∂f / ∂y).
In addition, the derivatives of some common functions are useful to know. See the table of derivatives.
As an example, the derivative of
- <math>f(x) = 2x^4 + \sin (x^2) - \ln (x)\;e^x + 7<math>
is
- <math>f'(x) = 8x^3 + 2x\cos (x^2) - (1/x)\;e^x - \ln (x)\;e^x.<math>
Using derivatives to graph functions
Derivatives are a useful tool for examining the graphs of functions. In particular, the points in the interior of the domain of a real-valued function which take that function to local extrema will all have a first derivative of zero. However, not all critical points are local extrema; for example, f(x)=x3 has a critical point at x=0, but it has neither a maximum nor a minimum there. The first derivative test and the second derivative test provide ways to determine if the critical points are maxima, minima or neither.
In the case of multidimensional domains, the function will have a partial derivative of zero with respect to each dimension at local extrema. In this case, the Second Derivative Test can still be used to characterize critical points, by considering the eigenvalues of the Hessian matrix of second partial derivatives of the function at the critical point. If all of the eigenvalues are positive, then the point is a local minimum; if all are negative, it is a local maximum. If there are some positive and some negative eigenvalues, then the critical point is a saddle point, and if none of these cases hold then the test is inconclusive (e.g., eigenvalues of 0 and 3).
Once the local extrema have been found, it is usually rather easy to get a rough idea of the general graph of the function, since (in the single-dimensional domain case) it will be uniformly increasing or decreasing except at critical points, and hence (assuming it is continuous) will have values in between its values at the critical points on either side.
Generalizations
Where a function depends on more than one variable, the concept of a partial derivative is used. Partial derivatives can be thought of informally as taking the derivative of the function with all but one variable held temporarily constant near a point. Partial derivatives are represented as ∂/∂x (where ∂ is a rounded 'd' known as the 'partial derivative symbol'). Some people pronounce the partial derivative symbol as 'der' rather than the 'dee' used for the standard derivative symbol, 'd'.
The concept of derivative can be extended to more general settings. The common thread is that the derivative at a point serves as a linear approximation of the function at that point. Perhaps the most natural situation is that of functions between differentiable manifolds; the derivative at a certain point then becomes a linear transformation between the corresponding tangent spaces and the derivative function becomes a map between the tangent bundles.
In order to differentiate all continuous functions and much more, one defines the concept of distribution.
For complex functions of a complex variable differentiability is a much stronger condition than that the real and imaginary part of the function are differentiable with respect to the real and imaginary part of the argument. For example, the function f(x + iy) = x + 2iy satisfies the latter, but not the first. See also Holomorphic function.
See also
- table of derivatives
- differintegral
- covariant derivative
- Lie derivative
- exterior derivative
- exterior covariant derivative
- derivation (abstract algebra)
- Fréchet derivative
- Gâteaux derivative
- functional derivative
- Kähler differential
- Pincherle derivative
- partial derivative
- directional derivative
- total derivative
- convective derivative
- pushforward
- Schwarzian derivative
- Automatic differentiation
- derivative (examples)
- Matrix calculus
External links
- WIMS Function Calculator (http://wims.unice.fr/wims/wims.cgi?module=tool/analysis/function.en) makes online calculation of derivatives.
References
- Larson, Ron; Hostetler, Robert P.; and Edwards, Bruce H. (2003). Calculus of a Single Variable: Early Transcendental Functions (3rd edition). Houghton Mifflin Company. ISBN 061822307X.
- Anton, Howard (1980). Calculus with analytical geometry.. New York:John Wiley and Sons. ISBN 0-471-03248-4.cs:Derivace
da:Differentialregning de:Differentialrechnung es:Función derivada eo:Diferenciala kalkulo fr:Dérivée he:נגזרת io:Derivado it:Derivata lt:Išvestinė nl:Afgeleide ja:微分 pl:Pochodna funkcji pt:Derivada ro:Derivată ru:Производная функция fi:Derivaatta sv:Derivata th:อนุพันธ์ tr:Türev ve Türevlenebilirlik zh:导数