|
|
In the mathematical subfield of numerical analysis a Bézier curve is a parametric curve important in computer graphics. A numerically stable method to evaluate Bézier curves is de Casteljau's algorithm.
Generalizations of Bézier curves to higher dimensions are called Bézier surfaces; the Bézier triangle is a special case.
Bézier curves are also formed by many common forms of string art, where strings are looped across a frame of nails.
| Contents |
History
Bézier curves were widely publicized in 1962 by the French engineer Pierre Bézier who used them to design automobile bodies. The curves were developed in 1959 by Paul de Casteljau using de Casteljau's algorithm.
Definition
Given n+1 points Pi in R3 a Bézier curve of degree n is a parametric curve
- <math>\mathbf{B}:[0,1] \to \mathbb{R}^3<math>
composed of Bernstein basis polynomials of degree n
- <math>\mathbf{B}(t)= \sum_{i=0}^n \mathbf{P}_{i} b_{i,n}(t) \mbox{ , } t \in [0,1]<math>
with the Bernstein basis polynomials defined as
- <math>b_{i,n}(t):= {n \choose i} t^i (1-t)^{n-i} \qquad \mbox{ , } i=0,\ldots n.<math>
(for the Bernstein polynomials we adopt the convention that 00 = 1)
Pi is called control point for the Bézier curve. A polygon can be constructed by connecting the Bézier points with lines, starting with P0 and finishing with Pn. This polygon is called the Bézier polygon.
Notes
- The starting point of the curve is P0 and the ending point is Pn
- The Bézier curve is completely contained in the convex hull of the control points.
- If and only if all control points lie on the curve it is a straight line.
- The start (end) of the curve is tangent to the first (last) section of the Bézier polygon.
- A curve can be split at any point into 2 subcurves, or into arbitrarily many subcurves, each of which is also a Bézier curve.
- A circle cannot be exactly formed by a Bézier curve. Not even a circular arc. (However, often a Bézier curve is an adequate approximation to a small enough circular arc).
- The curve at a fixed offset from a given Bézier curve ("parallel" to that curve, like the offset between tracks in a railroad) cannot be exactly formed by a Bézier curve (except in some trivial cases). However, there are heuristic methods that usually give an adequate approximation for practical purposes.
Examples
Linear Bézier curves
Bézier "curve" of degree 1:
Given two control points P0 and P1 a linear Bézier curve is just a straight line between those two points. The curve is given by
- <math>\mathbf{B}(t)=(1-t)\mathbf{P}_0 + t\mathbf{P}_1 \mbox{ , } t \in [0,1].<math>
Quadratic Bézier curves
Bézier curve of degree 2:
A quadratic Bézier curve is the path traced by the function B(t). For points A, B, and C,
- <math>\mathbf{B}(t) = (1 - t)^{2}\mathbf{A} + 2t(1 - t)\mathbf{B} + t^{2}\mathbf{C} \mbox{ , } t \in [0,1].<math>
TrueType fonts use Bézier splines composed of the quadratic Bézier curves.
Cubic Bézier curves
Bézier curve of degree 3:
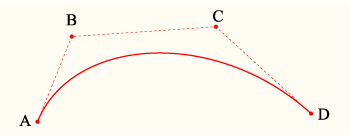
Four points A, B, C and D in the plane or in three-dimensional space define a cubic Bézier curve. The curve starts at A going toward B and arrives at D coming from the direction of C. In general, it will not pass through B or C; these points are only there to provide directional information. The distance between A and B determines "how long" the curve moves into direction B before turning towards D.
The parametric form of the curve is:
- <math>\mathbf{B}(t)=\mathbf{A}(1-t)^3+3\mathbf{B}t(1-t)^2+3\mathbf{C}t^2(1-t)+\mathbf{D}t^3 \mbox{ , } t \in [0,1].<math>
Modern imaging systems like PostScript, Metafont and GIMP use Bézier splines composed of cubic Bézier curves for drawing curved shapes.
Application in computer graphics
Bézier curves are widely used in computer graphics to model smooth curves. As the curve is completely contained in the convex hull of its control points, the points can be graphically displayed and used to manipulate the curve intuitively. Affine transformations such as translation, scaling and rotation can be applied on the curve by applying the respective transform on the control points of the curve.
The most important Bézier curves are quadratic and cubic curves. Higher degree curves are more expensive to evaluate and there is no analytic formula to calculate the roots of polynomials of degree 5 and higher. When more complex shapes are needed low order Bézier curves are patched together (obeying certain smoothness conditions) in the form of Bézier splines.
The following code is a simple practical example showing how to plot a cubic Bezier curve in C. Note, this simply computes the coefficients of the polynomial and runs through a series of t values from 0 to 1 - in practice this is how it is usually done, even though neat algorithms such as deCasteljau's are often cited in graphics discussions, etc. This is because in practice a linear algorithm like this is faster and less resource-intensive than a recursive one like deCasteljau's. The following code has been factored to make its operation clear - an optimization in practice would be to compute the coefficients once and then re-use the result for the actual loop that computes the curve points - here they are recomputed every time, which is less efficient but helps to clarify the code.
The resulting curve can be plotted by drawing lines between successive points in the curve array - the more points, the smoother the curve.
/******************************************************
Code to generate a cubic Bezier curve
Warning - untested code
*******************************************************/
typedef struct
{
float x;
float y;
}
Point2D;
/******************************************************
cp is a 4 element array where:
cp[0] is the starting point, or A in the above diagram
cp[1] is the first control point, or B
cp[2] is the second control point, or C
cp[3] is the end point, or D
t is the parameter value, 0 <= t <= 1
*******************************************************/
Point2D PointOnCubicBezier( Point2D* cp, float t )
{
float ax, bx, cx;
float ay, by, cy;
float tSquared, tCubed;
Point2D result;
/* calculate the polynomial coefficients */
cx = 3.0 * (cp[1].x - cp[0].x);
bx = 3.0 * (cp[2].x - cp[1].x) - cx;
ax = cp[3].x - cp[0].x - cx - bx;
cy = 3.0 * (cp[1].y - cp[0].y);
by = 3.0 * (cp[2].y - cp[1].y) - cy;
ay = cp[3].y - cp[0].y - cy - by;
/* calculate the curve point at parameter value t */
tSquared = t * t;
tCubed = tSquared * t;
result.x = (ax * tCubed) + (bx * tSquared) + (cx * t) + cp[0].x;
result.y = (ay * tCubed) + (by * tSquared) + (cy * t) + cp[0].y;
return result;
}
/*****************************************************************************
ComputeBezier fills an array of Point2D structs with the curve points
generated from the control points cp. Caller must allocate sufficient memory
for the result, which is <sizeof(Point2D) * numberOfPoints>
******************************************************************************/
void ComputeBezier( Point2D* cp, int numberOfPoints, Point2D* curve )
{
float t, dt;
int i;
dt = 1.0 / ( numberOfPoints - 1 );
for( i = 0, t = 0; i < numberOfPoints; i++, t += dt)
curve[i] = PointOnCubicBezier( cp, t );
}
Rational Bézier curves
Some curves that seem simple, like the circle, cannot be described by a Bézier curve or a piecewise Bézier curve (though in practice the difference is small and may be tolerable). To describe some of these other curves, we need additional degrees of freedom.
The rational Bézier curve adds weights that can be adjusted. The numerator is a weighted Bernstein form Bézier curve and the denominator is a weighted sum of Bernstein polynomials.
Given n+1 control points Pi, the rational Bézier curve can be described by:
- <math>
\mathbf{B}(t) = \frac{ \sum_{i=0}^n b_{i,n}(t) \mathbf{P}_{i}w_i } { \sum_{i=0}^n b_{i,n}(t) w_i } <math> or simply
- <math>
\mathbf{B}(t) = \frac{ \sum_{i=0}^n {n \choose i} t^i (1-t)^{n-i}\mathbf{P}_{i}w_i } { \sum_{i=0}^n {n \choose i} t^i (1-t)^{n-i}w_i }. <math>
See also
References
- Paul Bourke: Bézier curves, http://astronomy.swin.edu.au/~pbourke/curves/bezier/
- Donald Knuth: Metafont: the Program, Addison-Wesley 1986, pp. 123-131. Excellent discussion of implementation details; available for free as part of the TeX distribution.
- Dr. Thomas Sederberg, BYU Bézier curves,http://www.tsplines.com/tutorials/ch2.pdf
External links
- Living Math Bézier applet (http://www.sunsite.ubc.ca/LivingMathematics/V001N01/UBCExamples/Bezier/bezier.html)
- Living Math Bézier applets of different spline types, JAVA programming of splines (http://www.ibiblio.org/e-notes/Splines/Bezier.htm) in An Interactive Introduction to Splines (http://ibiblio.org/e-notes/Splines/Intro.htm)
- Don Lancaster's Cubic Spline Library (http://www.tinaja.com/cubic01.asp) describes how to approximate a circle (or a circular arc, or a hyperbola) by a Bézier curve; using cubic splines for image interpolation, and a explanation of the math behind these curves.cs:Bézierova křivka
de:Bézierkurve fr:Courbe de Bézier ko:베지에 곡선 ja:ベジェ曲線 lt:Bezjė kreivė pl:Krzywa Beziera sl:Bézierjeva krivulja